Glossary

Acquisition of Signal (AOS)

The signal time when a GroundStation comes in contact with a spacecraft. See the discussion of the Spacecraft.PassData method on the Interval Methods page of the Coverage and Contact Analysis guide for more information.

Air Force Satellite Control Network (AFCN)

A network of tracking stations contained in the Station Geodetics File.

Alfano/Negron Close Approach Software (ANCAS)

The ANCAS interpolation algorithms are used in the Spacecraft.CloseApproachRange Method to compute the associated times and ranges.

Attitude History File (AHF)

The attitude history file object is an Ephemeris object which stores a list of data records containing the orientation of a Spacecraft at specific epochs.

Annular Shadow

The conical part of a shadow, cast by a celestial body, which is beyond the intersection of the rays forming the umbra region, but within that of the penumbra region. See the discussion of the Spacecraft.ShadowTimes method on the Interval Methods page of the Coverage and Contact Analysis guide for more information.

Application Program Interface (API)

An interface by which external software can interact with an engine typically contained within another piece of individual software. Typically an API is offered in the form of dynamic link libraries (DLLs) that a software's code base can reference. For information on the FreeFlyer API, see the Application Program Interface page.

Apoapsis

Point farthest from the prime focus in an elliptical orbit. See related property and method: Spacecraft.Apoapsis and Spacecraft.OrbitApoapsis. For information on stepping to this condition, see the Stepping the Spacecraft page of the Spacecraft Propagation guide.

Apogee

The farthest point in an elliptical orbit about the Earth. See related property and method: Spacecraft.Apogee and Spacecraft.OrbitApogee. For information on stepping to this condition, see the Stepping the Spacecraft page of the Spacecraft Propagation guide.

Apogee Height

The instantaneous osculating value of the distance of the farthest point in the orbit above an oblate Earth based on the “WGS 1984” spheroid.

Apsidal Line

The line connecting the periapsis with the apoapsis. See Eccentric Anomaly.

Argument of Latitude

The angle between the vector pointing to the ascending node and the vector pointing to the Spacecraft’s current position. The argument of latitude is the sum of the Keplerian elements true anomaly and argument of periapsis.

Argument of Periapsis

The angle, in the plane of the satellite’s orbit, between the ascending node and the periapsis point, measured in the direction of the satellite’s motion. See Keplerian Elements.

Argument of Perigee (W, ω)

The angle, in the plane of the satellite’s orbit, between the ascending node and the perigee point, measured in the direction of the satellite’s motion, and represented by W in Keplerian elements.

Ascending Node

The point at which the Spacecraft crosses the equatorial plane moving from the south to the north. For information on stepping to this condition, see the Stepping the Spacecraft page of the Spacecraft Propagation guide.

Azimuth (Az)

For a Spacecraft object, the angle in the horizontal plane from North to the projection of the velocity vector on the horizontal plane. State vector element in the Spherical and Spherical Lat/Long systems. For a GroundStation object, the angle between the projection of the GroundStation to Spacecraft vector on the GroundStation’s local tangent plane and the GroundStation’s geographic North vector.

Batch Least Squares (BLS)

In the general sense, least squares estimation is the approximation of a solution to an overdetermined system. The "batch" refers to the simultaneous approximation of multiple measurements. In FreeFlyer, BLS is used in orbit determination. The BatchLeastSquaresOD object is used to estimate the state of a Spacecraft using tracking data. See the guide on setting up Batch Least Squares in FreeFlyer.

Beta Angle

The angle between the orbit plane and the CentralBody-Sun vector. Related Property: Spacecraft.BetaAngle.

Blackjack Point Solution File

The Blackjack Point Solution File is an ASCII file of Point Solution data as put out by the BlackJack GPS receiver. The time system is GPS Time, and the position and velocity values are given in the Earth Fixed reference frame. See the guide on Tracking Data File Formats for more information.

Body Coordinate System (BCS)

The Body Coordinate System is an orthogonal, right handed coordinate system attached to (translates with and rotates with) the spacecraft. In FreeFlyer, the attitude of the spacecraft is synonymous with the orientation of the BCS. To define the orientation of the BCS, one needs to specify an attitude reference frame from which the BCS is oriented.

B-Plane Coordinate System

The B-plane is a target plane that slices through the center of the Celestial Body. The normal (referred to as the S-axis) of the B-plane is parallel to the incoming asymptote of a hyperbolic trajectory. The T-axis of the coordinate system is obtained by taking a normalized cross-product of the S-axis and the Celestial Body’s orbit normal and the R-axis completes the right-handed triad in the sense of (R, S, T). Although the coordinate system and the associated piercing point parameters can be evaluated at almost any point on a Spacecraft’s trajectory, the B-plane parameters are only meaningful when the Spacecraft has stopped on the point of closest approach to the Celestial Object (i.e. periapsis). The B-plane is used extensively in targeting close encounters with Celestial Bodies (planets and their moons) for capture or gravity assist missions. Of particular interest is the set of parameters that define where a spacecraft’s hyperbolic trajectory pierces the B-plane. FreeFlyer Spacecraft object methods in this set are: BPlaneBMag, BPlaneBdotT, BPlaneBdotR, and BPlaneTheta. For an example, see the B-Plane Targeting Sample Mission Plan.

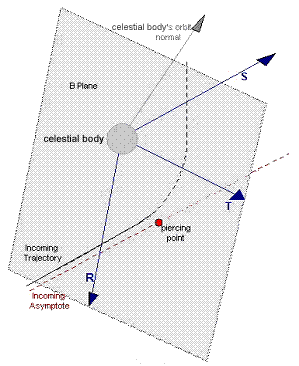B-Plane Coordinate System

Boresight

Boresight is nominally defined as the "center" or principle axis of a sensor. It is the reference point from which sensor measurements are made.

Brouwer-Lyddane

Brouwer theory provides a rapid means of determining a satellite ephemeris. This theory was modified by Lyddane to obtain algorithms applicable for zero eccentricity and zero inclination. Brouwer and Brouwer-Lyddane theory require a specific set of elements (Goddard Trajectory Determination System Mathematical Theory Revision 1), Flight Dynamics Division Code 500, 1989).

Brouwer-Lyddane Mean Elements

The Brouwer-Lyddane Mean elements use the Brouwer orbit theory, with updates by Lyddane to handle small eccentricities and inclinations, to calculate mean elements. The Brouwer-Lyddane elements use the same element representation as the Keplerian elements. The mean anomaly is used instead of the true anomaly for the Brouwer representations. The Keplerian element set used is osculating, (i.e., they give the satellite’s exact position and velocity at a given instant in time); the Brouwer-Lyddane elements average out much of the effects of osculations, producing a mean representation of the orbit. Brouwer orbit theory provides an analytic solution for the position and velocity of a satellite orbiting a central body, where the central body is modeled as a point mass with perturbations from the zonal harmonics J2 through J5. The 6 elements are represented as functions of time, where each function consists of the corresponding Keplerian element plus time varying perturbation terms. The mean elements of the satellite may be computed by solving the Brouwer-Lyddane analytic equations at any desired time. The Brouwer-Lyddane mean elements may then be converted to ordinary Keplerian elements to get the satellite’s instantaneous orbital state.

Bulirsch Stoer

The Bulirsch Stoer propagator is a self-starting single step integrator that is designed to take very large steps compared to the Runge-Kutta propagators at comparable accuracy. It is applicable to ForceModels that are very smooth. See the guide on Spacecraft Propagators for more information on FreeFlyer integrators.

Bulirsch Stoer VOP

The Bulirsch Stoer VOP propagator is based on a Variation of Parameters (VOP) formulation of the equations of motion in equinoctial elements. It may be used when the ForceModel is very smooth. See the guide on Spacecraft Propagators for more information on FreeFlyer integrators.

Cd

The drag coefficient, one of the Spacecraft physical properties.

Cl

The lift coefficient, one of the Spacecraft physical properties.

Cr

The reflectivity coefficient, one of the Spacecraft physical properties.

Cardinal Points

The cardinal point calculations are based on the alpha angle, which is the angle between the Spacecraft's position and the target CelestialObject's position with respect to the Spacecraft's central body when both vectors are projected onto the Spacecraft's orbit plane. Note that the target CelestialObject is modeled as a point. The cardinal points, as a function of the alpha angle, are defined as follows. See related methods: Spacecraft.CardinalPoints or the Cardinal Points Sample Mission Plan.

Cartesian

Cartesian elements define the position and velocity of a spacecraft with respect to the origin of an inertial rectangular coordinate system. Positions and velocities are expressed by their components along the three principal axes of this system. Within FreeFlyer, spacecraft trajectory elements are handled in ICRF Cartesian Coordinates and expressed in metric units. This is the coordinate system used for event calculations, orbit propagation and report generation. More flexibility has been given to the user, via the capability to select different coordinate systems. The system performs the required coordinate transformations and generates the requested data in these systems. Position, Velocity, and Acceleration are vectors, where the X, Y, and Z directions are set by the coordinate system selection. Their individual components can be accessed using individual elements, e.g. the X component of position is reported using the X element. The Input/Output properties for this set are: X, Y, Z, VX, VY, VZ.

Code 500 (C500) Ephemeris File

The Code 500 Ephemeris File is an ephemeris-file format for use with many NASA applications. This format is used mostly at the Goddard Space Flight Center (GSFC). This format can be used for both input and output of Spacecraft orbital data. The Ephemeris object allows you to store the state of a Spacecraft, at fixed time intervals during the mission, to a binary file. When the data is stored in a file, FreeFlyer and a host of GSFC/NASA software systems can import the data and perform calculations on the trajectory information. See the Working with Ephemerides guide for more information about creating and importing a Code 500 Ephemeris file.

Constellation

A group of Spacecraft with orbits spaced in a specific pattern, generally designed to achieve coverage of regions on the Earth. FreeFlyer handles groups of Spacecraft with the Formation object.

Consultative Committee for Space Data Systems Orbit Ephemeris Message (CCSDSOEM) File

The Consultative Committee for Space Data Systems (CCSDS) produces an Orbit Ephemeris Message (OEM) containing a series of state vectors for a single object. The CCSDS OEM is an ASCII text file containing a header, Metadata, explanatory information (optional comments), and ephemeris data. See the Working with Ephemerides guide for more information about creating and importing a Code 500 Ephemeris file.

Coordinated Universal Time (UTC)

Coordinated Universal Time. UTC time matches TAI time within an integral number of one-second offsets inserted to make the time system’s local midnight match the observed local midnight to within +/- 0.9 seconds. UTC time differs from TAI time by an integral number of leap seconds. The time difference between UTC and TAI times occurs because of variations in the rotational rate of the Earth. Astronomical observations are used to determine the drift of the Earth’s rotation, and these observations are used to calculate the insertion of an additional second into the offset between TAI and UTC times. These leap seconds are calculated at the Naval Observatory in Washington. DC, and published in tables at regular intervals. The most recent table of actual and predicted leap seconds is contained for use in calculating time system conversions. See the Parsing Dates and Times guide for more information.

Cowell

The Cowell propagator is a numerical integrator using a predictor-corrector approach. While faster than Runge-Kutta propagators, it requires ForceModels that are very smooth. See the guide on Spacecraft Propagators for more information on FreeFlyer integrators.

Custom Observation

is A unique set of measurements, either natively supported measurements or a custom set of measurements, used to estimate the state of a Spacecraft during Orbit Determination by computing computed observables and being compared with observed observables. Custom Observations can be used with BatchLeastSquaresOD, KalmanFilterOD , UnscentedKalmanFilterOD, and SquareRootInformationFilterOD.

Declination (Dec)

Angle between the spacecraft radius vector and the equatorial plane. Element in the Spherical system state vector.

Deep Space Network 60-Byte (DSN60) Observation File

The DSN 60-Byte Observation File is a GSFC internal 60-byte binary format. Each file of DSN 60-byte tracking data contains one or more header records and an associated batch of data records accompanying each header record – the header record containing information necessary for the accurate conversion of the raw data contained in the data records. The time system is UTC, and the range and range-rate data is reference frame independent. The format for this data type is specified in the GSFC document "60-Byte Data Format Definition", Revision 2, May 1994. See the Tracking Data File Formats guide for more information.

Descending Node

The point at which the Spacecraft crosses the equatorial plane moving from the north to the south. For information on stepping to this condition, see the Stepping the Spacecraft page of the Spacecraft Propagation guide.

Database Management Systems (DBMS)

DBMS interaction with FreeFlyer is provided through Structured Query Language (SQL). See the Databases guide for more information.

Differential Corrector Method

A differential corrector process consists of first making small variations, or perturbations, to input properties. The resulting changes in the outputs are measured to determine the relationship to the changes in the inputs. These changes are referred to as the sensitivity matrix (also called the Jacobean matrix). In a process that uses the inverse of the sensitivity matrix, the input properties are tuned so that the outputs move closer to the goals. This method usually requires several iterations to obtain the goals. Its ability to find a solution that meets the goals within a defined tolerance, or converges, depends on the sensitivity matrix's capability to be inverted. In FreeFlyer, the DifferentialCorrector object is used by a targeting loop to adjust input properties of a user-defined process in an attempt to make the output of that process match a specific set of goals. For more information, see an example in the Targeting guide.

Dynamic-Link Library (DLL)

A library of linked and compiled code that can be referenced by another piece of code to enable functionality transmission between code-bases.

Deep Space Network (DSN)

A network of NASA tracking stations contained in the Station Geodetics File.

Eccentricity (e)

A parameter that defines the shape of a conic orbit, the difference in the apogee and perigee divided by their sum. Part of the Keplerian element set.

Eccentric Anomaly (E, EA)

The angle at the center of an elliptical orbit formed by the apsidal line and the radius vector drawn from the center to the point on the circumscribing auxiliary circle from which a perpendicular to the apsidal line will intersect the Spacecraft position. See related property: Spacecraft.EA.

Eccentricity Vector

A unit vector that points from the center of the Earth towards perigee with a magnitude equal to the eccentricity of the orbit. See related property: Spacecraft.EVector.

Elevation (El)

For a GroundStation object, the angle between the GroundStation-to-Spacecraft vector and the GroundStation’s local horizontal plane, tangent to the WGS 1984 reference Earth spheroid. For a Spacecraft object, the angle between the Spacecraft-to-target vector and the x-y plane of the Spacecraft. See the Contact Methods guide for more information.

Equinoctial Elements

Element set that handles point singularities. Singularities occur in the Keplerian elements when the inclination or eccentricity is zero. These coordinate singularities occur because at zero degrees inclination, the line of nodes is not defined, and at eccentricity = 0, the apogee and perigee points are not defined, which implies that the values of the Keplerian elements Ω and ω for zero inclination, and elements ω for zero eccentricity, are not defined. In practice, numerical singularities are encountered if i<0.01 or e<0.00001. The equinoctial elements are a trigonometric combination of Keplerian elements, used to remove some of the singularities encountered in the Keplerian representation. Singularities are limited to retrograde equatorial orbit and parabolic/hyperbolic orbits. The input/output Spacecraft object properties for this set are: EquinoctialA, EquinoctialH, EquinoctialK, EquinoctialP, EquinoctialQ, EquinoctialLongitude.

Error Tolerance

Error tolerance is used in the propagation of a Spacecraft state within FreeFlyer. Intermediate integration steps are taken to ensure that the local error never exceeds the error tolerance value. In FreeFlyer, the error tolerance is compared to either the absolute error or relative error depending on the settings of the integrator. The absolute error is determined by taking the difference between two different order propagators. For example, an RK89 integrator uses the 8th order Runge-Kutta propagation with 9th order error control. The relative error is determined by dividing the absolute error by the change in the Spacecraft's state.

Extensible Markup Language (XML)

XML is the language used by FreeFlyer for the Mission Plan and object export files.

Field of View (FOV)

The field of view of an object refers to what it is able to 'see', or in other words sense. In FreeFlyer, Sensor objects have fields of view, and GroundStation objects also have fields of view based on their mask.

Geocentric Inertial Coordinate System (GCI)

GCI is the Geocentric Inertial coordinate system, also known as J2000, Mean of J2000, Mean of J2000 Earth Equator, ICRF, or ECI. It is the default inertial coordinate system used in FreeFlyer, a coordinate system located at the center of the Earth that does not rotate with the Earth. For a more detailed definition, see ICRF. See the Orbit Reference Frames and Attitude Reference Frames guides for more information.

Geodetic Spacecraft Attitude Reference Frame

The origin of the coordinate system is the center of the spacecraft. The y axis is in the opposite direction of the orbit normal. The z axis is pointed along the line drawn from the spacecraft, which is perpendicular to the tangent point on the Earth’s surface. The x axis is the vector perpendicular to the y and z axes, which forms a right-handed coordinate system. See the attitude reference frames section on the geodetic coordinate system.

Geosynchronous Orbit

The Geosynchronous Orbit Type sets up the spacecraft orbit to travel at the same rate of the earth's rotation. A satellite in Geosynchronous orbit circles the earth once each day. For a satellite's orbit period to be one sidereal day, its height must be approximately 35,786 kilometers above the earth's surface.

Semimajor Axis: A = ((t√μ)/ 2π)2/3

Given:

•μ = 398600.5

•t = 86400 sec

•A ≈ 42241 km

For a geostationary orbit--a special type of geosynchronous orbit where the satellite stays over the same spot on earth--the orbit has to be circular and remain directly above the equator. Otherwise, from the earth the satellite would appear to move. Thus, both the eccentricity and inclination are near zero for a geostationary satellite. FreeFlyer includes an Orbit Wizard that allows you to easily create Geosyncronous orbits.

Greenwich Hour Angle (GHA)

Angular distance west of the Greenwich celestial meridian; the arc of the celestial equator, or the angle at the celestial pole, between the upper branch of the Greenwich celestial meridian and the hour circle of a point on the celestial sphere (the x-axis of the Mean of J2000 Earth-Equator coordinate frame), measured westward from the Greenwich celestial meridian through 360 degrees; local hour angle at the Greenwich meridian. See related property: Spacecraft.GHA.

Greenwich Apparent Sidereal Time (GAST)

Sidereal time is a system of timekeeping based on the rotation of the Earth with respect to the fixed stars in the sky. Specifically, it is the measure of the hour angle of the vernal equinox. If the hour angle is measured with respect to the mean equinox, mean sidereal time is being measured, and if the hour angle is measured with respect to the true equinox, apparent sidereal time is being measured. When the measurement is made with respect to the meridian at Greenwich, the time is referred to as Greenwich mean sidereal time (GMST) and Greenwich apparent sidereal time (GAST). See related method: CelestialObject.GetPrimeMeridianApparentSiderealTime()

Global Positioning Satellite (GPS) Pivot Point Solution File

The GPS Pivot Point Solution File is an ASCII file of Point Solution data as put out by the Pivot GPS receiver. The time system is TAI, and position and velocity values are given in ICRF. For more information see the Tracking Data File Formats guide.

Graphical User Interface (GUI)

A GUI is anything that is used as a visual connection between inputs and a software operation. Examples of GUIs in FreeFlyer are the windows interfaced with when using FreeFlyer.exe, the UserInterface object, and the object dialogs in the Control panel.

Harris-Priester Atmospheric Density Model

A method for modeling atmospheric density; used in spacecraft drag calculation. The Harris-Priester Drag File provides the data file for 1964 Harris – Priester Atmospheric density modeling. A table of integral flux values (measured at F10.7 = 65,75,100,125,150,175,200,225,250,275 x10-22 W/m2/Hz) provides the atmospheric density for altitudes between 0 and 2000 kilometers. See the Atmospheric Forces section of the Spacecraft Propagation guide for more information.

Hill-Clohessy-Wiltshire (HCW) Equations of Motion

The HCW equations of motion are linearized equations that describes the motion of a body relative to a reference orbit that is circular or nearly circular without disturbance forces. See the Relative Motion section of the Spacecraft Propagation guide for more information.

Horizontal Flight Path Angle (HFPA)

Complement to the VFPA, the HFPA is the angle between the velocity vector and the vector perpendicular to the spacecraft position vector. This is an element in the Spherical Lat/Long system state vector.

Inclination (I, i)

Inclination of the conic representing the orbit in the Keplerian(I), Brouwer-Lyddane Mean, J2 Brouwer-Lyddane, and SGP4 systems. The angle between the equatorial plane and the orbit plane at the ascending node.

International Atomic Time (TAI)

TAI time is measured in seconds from a reference epoch. The time system is continuous; there are no discontinuities related to variations in the environment. The time difference between UTC and TAI times occurs because of variations in the rotational rate of the Earth. Astronomical observations are used to determine the drift of the Earth’s rotation, and these observations are used to calculate the insertion of an additional second into the offset between TAI and UTC times. These leap seconds are calculated at the Naval Observatory in Washington. DC, and published in tables at regular intervals. The most recent table of actual and predicted leap seconds is contained for use in calculating time system conversions. See the Parsing Dates and Times guide for more information.

International Celestial Reference Frame (ICRF)

The International Celestial Reference Frame (ICRF) is a fundamental reference frame defined by the the International Astronomical Union (IAU). The ICRF is considered the best realization of an inertial frame constructed to date, representing improvement upon the theory behind the J2000 frame. The ICRF axes are not dependent on the motion or orientation of the Earth, unlike the Mean of J2000 reference frame which depends on the Earth's equatorial and ecliptic planes.

The transformation between the inertial ICRF frame and earth fixed ITRF frame is computed in FreeFlyer using the Standards of Fundamental Astronomy (SOFA) Tools for Earth Attitude software library. By default, FreeFlyer uses an interpolated version of the IAU 2006/2000A earth orientation model but users can also access to the IAU 2006/2000B model. The IAU 2006/2000A and IAU 2006/2000B precession/nutation models and the Earth rotation angle are documented by IERS in the Technical Note No. 32, IERS Conventions 2003 and the Technical Note No. 36, IERS Conventions 2010.

International Reference Ionosphere (IRI) Model

The IRI Model is used to model the effects of ionospheric refraction. In FreeFlyer the model properties are configured using the IonosphereOptions object.

Interval Method

A method used in conjunction with the step command to output "event" times. It functions by "stepping" to the event (such as OrbitApogee), outputting the time, then stepping to the next occurrence of the event. For a list of Interval Methods, see the Interval Methods reference.

J2 Brouwer-Lyddane Elements

The J2 Brouwer-Lyddane elements use the Brouwer orbit theory, with updates by Lyddane to handle small eccentricities and inclinations, to convert osculating Keplerian elements to mean-only Keplerian elements. The J2 implementation is a special implementation of the Brouwer-Lyddane theory that uses J2 only as its perturbing acceleration; the remaining J terms (J3, J4, and J5) are set to zero. This implementation was found to closely match the numerical averaging formulations for calculating mean elements. That is particularly useful for specific types of analysis. These calculations simplify the conversion between mean and osculating elements for frozen orbit analysis.

Jacchia Roberts (JR) Atmospheric Density Model

A method for computing atmospheric density; used in the spacecraft drag calculation. FreeFlyer can use either the NOAA Jacchia-Roberts Drag File (which models atmospheric density variations based on historical data), the Schatten Solar Flux Prediction Files, or a user created file. See the Atmospheric Forces section of the Spacecraft Propagation guide for more information.

Jacobian

The Jacobian matrix of any vector-valued function is the matrix of all of its first-order partial derivatives. In the context of an optimization process, the Jacobian contains the partial derivatives of each Constraint with respect to each State Variable. Each row of the Jacobian corresponds to a Constraint, and each column corresponds to a State Variable. See the Specifying Known Derivatives section of the Optimization guide for more information.

Kalman Filter

A set of mathematical equations that provide an efficient means to estimate state of a system from measurements that contain random errors. In FreeFlyer, the Kalman Filter has been applied to the Orbit Determination process. The KalmanFilterOD and UnscentedKalmanFilterOD objects contain the algorithms to estimate the state vector of a Spacecraft orbit from tracking station data. Learn more in the Orbit Determination guide.

Keplerian Elements

These classical elements provide insight into the spacecraft orbit by completely describing the size, shape and orientation of the orbit, and the position of the satellite in the orbit. The semi-major axis and eccentricity define the size and shape of the orbit. The inclination, right ascension of ascending node, and argument of perigee define the orientation of the orbit. The final property, the true anomaly, defines where the satellite is located in the orbit. The system is designed to describe elliptical orbits. The Input/Output properties for this set are: A, E, I, RAAN, W, TA. See the Orbit Element Types guide for more information.

L1-centered RLP Coordinate System

The L1-centered RLP coordinate system is the natural frame for describing the dynamical motion in the circular restricted three-body problem about the interior collinear Lagrange point, L1. The two gravitational centers used in the calculations can be defined by the user as any CelestialObject or barycenter where the L1 point is between the primary system (P1) and the secondary system (P2) and lies on the line joining them. By definition the frame is non-inertial and rotates at the same rate as P2 and P1 move about their common barycenter. See the Rotating Libration Point guide for more information.

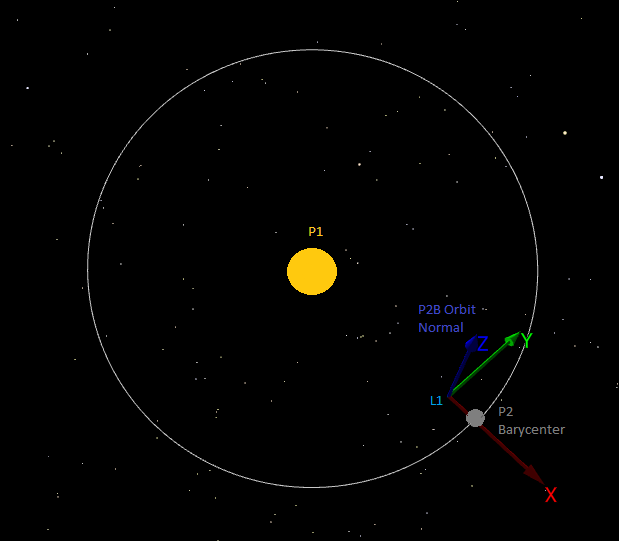L1-Centered RLP Coordinate System

L2-centered RLP Coordinate System

The L2-centered RLP coordinate system is the natural frame for describing the dynamical motion in the circular restricted three-body problem about the interior collinear Lagrange point, L2. The two gravitational centers used in the calculations can be defined by the user as any Celestial Object or barycenter where the L2 point lies on the line joining the primary system (P1) and the secondary system (P2) and is located further from P1 than P2. By definition the frame is non-inertial and rotates at the same rate as P2 and P1 move about their common barycenter. See the Rotating Libration Point guide for more information.

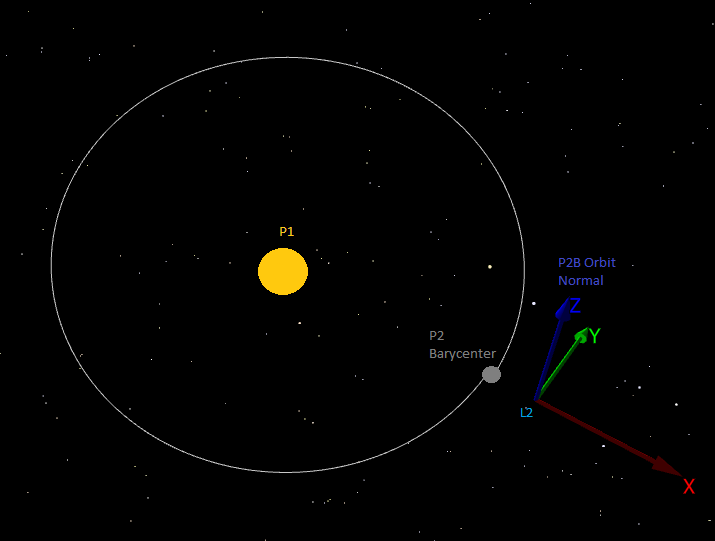L2-Centered RLP Coordinate System

L3-centered RLP Coordinate System

The L3-centered RLP coordinate system is the natural frame for describing the dynamical motion in the circular restricted three-body problem about the interior collinear Lagrange point, L3. The two gravitational centers used in the calculations can be defined by the user as any Celestial Object or barycenter where the L3 point lies on the line joining the primary system (P1) and the secondary system (P2) and is located further from P2 than P1. By definition the frame is non-inertial and rotates at the same rate as P2 and P1 move about their common barycenter. See the Rotating Libration Point guide for more information.

L3-Centered RLP Coordinate System

L4-centered RLP Coordinate System

The L4-centered RLP coordinate system is the natural frame for describing the dynamical motion in the circular restricted three-body problem about the triangular Lagrange point, L4. The two gravitational centers used in the calculations can be defined by the user as any Celestial Object or barycenter where the L4 point lies at the third corner of the equilateral triangle whose base joins the primary system (P1) and the secondary system (P2) and is located ahead of P2 in its orbit. By definition the frame is non-inertial and rotates at the same rate as P2 and P1 move about their common barycenter. See the Rotating Libration Point guide for more information.

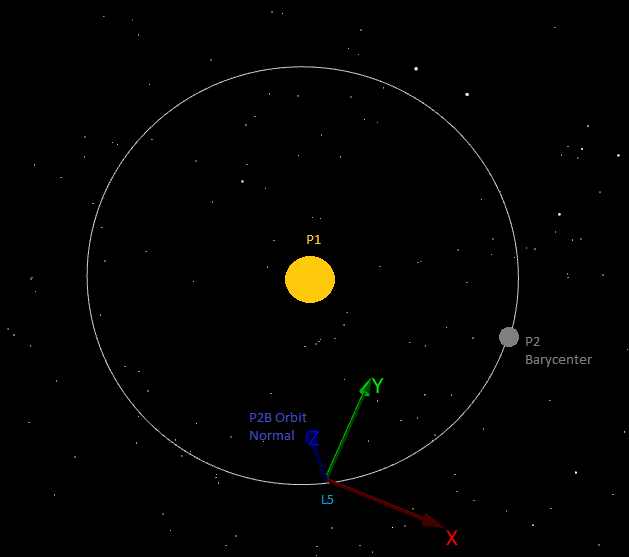
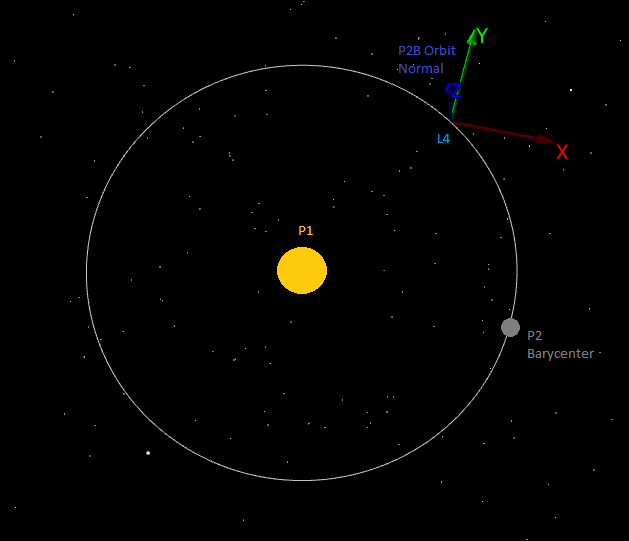L4-Centered RLP Coordinate System

L5-centered RLP Coordinate System

The L5-centered RLP coordinate system is the natural frame for describing the dynamical motion in the circular restricted three-body problem about the triangular Lagrange point, L5. The two gravitational centers used in the calculations can be defined by the user as any Celestial Object or barycenter where the L5 point lies at the third corner of the equilateral triangle whose base joins the primary system (P1) and the secondary system (P2) and is located behind P2 in its orbit. By definition the frame is non-inertial and rotates at the same rate as P2 and P1 move about their common barycenter. See the Rotating Libration Point guide for more information.

L5-Centered RLP Coordinate System

Latitude (Lat)

Geodetic latitude is the angle between the equatorial plane and the line through the spacecraft and normal to the geoid. This is an element in the Spherical Lat/Long state vector.

Launch Coordinate System

This system is designed to facilitate analysis of satellite launch. The z-axis is the north-pointing vector normal to the true equatorial plane at the reference epoch. The x-axis lies in the true equatorial plane at the reference epoch, and points from the center of the Earth to the reference longitude (launch site longitude) on the Earth’s surface. The y-axis is the vector perpendicular to the x- and z- axes, which forms a right-handed coordinate system. The origin of the coordinate system is set at the center of the Earth. The advantage of the launch coordinate system is that the launch vehicle trajectory can be designed without regard to launch time and date, which can be selected separately later to define the required range of right ascension of the ascending node (W) (RAAN). Launch coordinates have an associated reference longitude and epoch that the user defines. The reference epoch is usually set at the time of liftoff, and the longitude at the launch site longitude. The Cartesian element type is used when entering a state using the Launch Coordinate reference frame.

Local Vertical Local Horizontal (LVLH) Spacecraft Attitude Reference Frame

The origin of the LVLH coordinate system is the center of the Spacecraft. The y axis is in the opposite direction to the orbit normal (the orbit normal being in the direction of the vector product r x v). The z axis is in the opposite direction to the position vector r. The x axis forms a right-handed coordinate system.

Longitude (Long)

Geographic longitude of the Spacecraft sub-satellite point, east of the prime meridian, is an element in the Spherical Lat/Long state vector.

Longitude of Periapsis

The angle between the vernal equinox and periapsis. Used in calculation of mean geodetic longitude (MGL). See related property: Spacecraft.MGL.

Loss of Signal (LOS)

The signal time where a GroundStation loses contact with a Spacecraft. See the discussion of the Spacecraft.PassData method on the Interval Methods page of the Coverage and Contact Analysis guide for more information.

Manifolding

The association of Thrusters to Tanks for the propulsion system of a Spacecraft. FreeFlyer supports bi-propellant thrusters and allows the user to set Mix Ratios for each tank and Valves for each thruster-tank set. See the Valves section of the Maneuvering guide for more information.

Masking Profile

Azimuth and Elevation angle pairs used to describe the visibility for a Ground Station, or a Sensor. Possible Ground Station obstructions are landscapes, buildings, or a “keyhole”, a possible Sensor obstruction is a spacecraft component (i.e. solar array). The mask profile consists of an Elevation angle coupled to an Azimuth angle above which the visibility is unobstructed.

Mass Spectrometer Incoherent Scatter (MSIS) Radar Extended Model Files

The MSIS model uses the Celestrak Space Weather File by default, and can also use custom ASCII drag data files. These files can be used with the MSIS-2000, MSIS-90, MSIS-86, and Jacchia Roberts models. Although the Jacchia Roberts model uses Tc data, this can be derived from the F10.7 and Ap data contained in these files. For more information on the MSIS models, courtesy of the Naval Research Laboratory, navigate to the Geospace Science & Technology section under Branches.

Mean Anomaly (M, MA)

A parameter that relates position and time for any celestial object in a conic orbit, the mean anomaly is proportional to the area swept out by the focus-to-body line since the last periapsis event. See related property: Spacecraft.MA. See the Orbit Element Types guide for use of mean anomaly in various FreeFlyer orbit element sets.

Mean Geodetic Longitude (MGL)

The sum of the Mean Anomaly and the longitude of periapsis minus the Spacecraft.CentralBodyObject's prime meridian apparent sidereal time. See related property: Spacecraft.MGL.

Mean of J2000 (MJ2000) Earth Ecliptic Coordinate System

The z-axis is the vector normal to the ecliptic plane at Julian year 2000.0, pointing toward the Northern Hemisphere. The x-axis is the vector pointing from the center of the Earth to the mean vernal equinox at Julian year 2000.0. The y-axis is the vector perpendicular to the x- and z- axes, forming a right-handed coordinate system. The origin of the coordinate system is the center of the Earth. See the appropriate section of the orbit reference frame page.

Mean of J2000 (MJ2000) Earth Equator Spacecraft Attitude Reference Frame

This system is the principal coordinate system used by FreeFlyer for computation. The z-axis is the vector normal to the mean equatorial plane at Julian year 2000.0, pointing towards the Northern Hemisphere. The x-axis is the vector pointing from the center of the Earth to the mean vernal equinox at Julian year 2000.0. The y-axis is the vector perpendicular to the x- and z-axes, forming a right-handed coordinate system. The origin of the coordinate system is the center of the Earth. See the appropriate section of the orbit reference frame page. This system is also commonly referred to as ECI or GCI.

Mean Local Time (MLT)

Spacecraft local time referenced to the mean sun. It is defined as Greenwich Mean Time (GMT) plus the spacecraft longitude (where longitude is converted to time assuming 15 deg per hour). Related Spacecraft object properties and methods: MLT, MltAscendingNode, MltDescendingNode, MltAscendingNodeError, MltDescendingNodeError.

Mercator Projection Map

A 2D equidistant-cylindrical view of Spacecraft orbit based on the Mercator view of a celestial body. See the Map and 2D Map guides for more information.

Modified Julian Date (MJD)

Modified Julian Date. All FreeFlyer MJD's are referenced to the GSFC base, unless specified otherwise. GSFC MJD = USNO MJD - 29999.5. See the Parsing Dates and Times guide for more information.

Modified Equinoctial Orbital Elements

The modified equinoctial orbital elements are useful for trajectory analysis and optimization. They are valid for circular, elliptic, and hyperbolic orbits. There is no singularity for zero eccentricity and orbital inclinations of zero and 90 degrees, but, two components are singular for an inclination of 180 degrees. The input/output Spacecraft object properties for this set are: ModifiedEquinoctialP, ModifiedEquinoctialF, ModifiedEquinoctialG, ModifiedEquinoctialH, ModifiedEquinoctialK, ModifiedEquinoctialL.

Molniya Orbit

A Molniya orbit is highly elliptical, with an inclination of 63.4 degrees and an orbital period of about 12 hours. It was designed to maximize the time a spacecraft spends in view of the high latitudes of the Earth, as it spends most of its time in an "apogee dwell" above 30 degrees N latitude in two locations on opposite sides of the Earth. FreeFlyer includes an Orbit Wizard that allows you to easily create Molniya orbits. The equations used to set this Orbit Type are:

Semimajor Axis:

Given:

•μ = 398600.5

•t = 43200 sec

•A ≈ 26610 km

hp = height/altitude = User Input

Eccentricity:

RE = Radius of the Earth = 6378.136 km

Inclination:

•I ≈ 63.4395 deg

Right Ascension of the Ascending Node:

•RAAN = User Input (0-360 deg)

Argument of Perigee:

•W = ω = User Input (0-360 deg)

True Anomaly:

•TA = User Input (0-360 deg)

Nonsingular Keplerian Elements

Keplerian element sets contain singularities when the orbital eccentricity is zero or when the orbital inclination is zero. Spacecraft orbits with properties near these values can suffer from numeric instabilities when representing the orbital state with Keplerian elements. One coordinate system designed to avoid these problems is the nonsingular Keplerian system. This system consists of six properties built from combinations of the Keplerian elements on the Spacecraft object: NonSingularA, NonSingularE1, NonSingularE2, NonSingularE3, NonSingularE4, NonSingularE5.

North American Aerospace Defense Command (NORAD)

The NORAD developed the Two-Line Element (TLE) format for transmitting satellite Keplerian elements. NORAD maintains general perturbation element sets on all resident space objects. These element sets are periodically refined so as to maintain a reasonable prediction capability on all space objects and are referred to as SGP4 derived elements. It is important to note that not just any prediction model will suffice. The SGP4 derived element sets are "mean" values obtained by removing periodic variations in a particular way. In order to obtain good predictions, these periodic variations must be reconstructed (by the prediction model) in exactly the same way they were removed by the source. Hence, inputting SGP4 elements into a different model (even though the model may be more accurate or even a numerical integrator) will result in degraded predictions. The prediction models are documented in the Spacetrack Report No. 3, which can be found at http://celestrak.com. See the guide on Spacecraft Propagators for more information on FreeFlyer integrators.

Obscuration

An obscuration is anything that may block the view of the sensor such as solar arrays, other instruments or even the Spacecraft body. See the Sensors guide for more information on defining obscuration masks.

Occultation

The blockage of light by the intervention of another object; the moon can occult (block) the light from the sun. The VisibilityCalculator object enables visibility calculations based on one or more occulting bodies.

Orbit Determination (OD)

OD is a process by which an orbit for a Spacecraft is determined using variant routines such as a Kalman Filter or Batch Least Squares approach from base observations, and is used for cases where the truth orbit for a Spacecraft after maneuvers and such is unknown. See the Orbit Determination guide for more information.

Open Database Connectivity (ODBC)

ODBC is the Windows interface to database drivers, and is used by FreeFlyer to interface with local or network relational databases. See the Databases page of the Interfacing with External Resources guide for more information.

Orbital Elements

Six quantities that describe the size, shape and orientation of an orbit; used to calculate the position of a satellite in its orbit at any given time. For a description of the many orbital element systems included in FreeFlyer, see the Orbit Element Types guide.

Outgassing

Outgassing models the effect of accelerations due to a leaking thruster on a Spacecraft. The accelerations are modeled using an analytic exponential decay model. See the guide on outgassing events for the use in FreeFlyer.

Particle Flux

Particle flux is the omnidirectional flux of a specified particle typeor a specified energy level. FreeFlyer uses the NASA AP-8 and AE-8 particle flux maps which contain collected data of proton and electron fluxes in the Earth's radiation belt with energy ranges from 0.04 MeV to 7 MeV for electrons and from 0.1 MeV to 400 MeV for protons in order to calculate the flux. See related methods: Spacecraft.ParticleFlux, Spacecraft.ParticleFluxTimes. Also see relevant sample Mission Plans ISS Over SAA and Particle Flux Model. For more detailed information on the particle flux models, please see the Goddard Space Flight Center AE-8/AP-8 Radiation Belt Models.

Penumbra

The outer part of a conical shadow, cast by a celestial body, where the light from the Sun is partially blocked. See related method: Spacecraft.PenumbralShadowTimes.

Periapsis

The point nearest the prime focus of an ellipse. See related method: Spacecraft.OrbitPeriapsis. For information on stepping to this condition, see the Stepping the Spacecraft page of the Spacecraft Propagation guide.

Perigee

The closest point in the orbit about the Earth. See related property and method: Spacecraft.Perigee, Spacecraft.OrbitPerigee. For information on stepping to this condition, see the Stepping the Spacecraft page of the Spacecraft Propagation guide.

Perigee Height

The instantaneous osculating value of the distance of the closest point in the orbit above an oblate Earth based on the WGS 1984 spheroid. See related property: Spacecraft.PerigeeHeight.

Period

The time elapsing between two consecutive passages of a satellite through a characteristic point on its orbit. See related property: Spacecraft.Period.

Planetodetic Coordinate System

The origin of the coordinate system is the center of the body. The x axis is the vector perpendicular to the y and z axes, which forms a right-handed coordinate system. Planetodetic longitude is the same as planetocentric longitude increasing positively eastward from -180 to 180 degrees. The planetodetic latitude is tied to a reference ellipsoid and increases positively northward from -90 to 90 degrees.

Quaternion

The four-element vector defining Spacecraft attitude by relating the Spacecraft body coordinates to the orbital frame. See related property: Spacecraft.Quaternion. See the Attitude System guide for more information.

Right Ascension (RA)

Angle from the x-axis of the Earth Equatorial coordinate system (vernal equinox) to the projection of the spacecraft radius vector on the equatorial plane. Element in the Spherical system state vector.

Right Ascension of the Ascending Node (RAAN, Ω)

Right ascension of the ascending node of the conic representing the orbit in the Keplerian, Brouwer-Lyddane Mean, J2 Brouwer-Lyddane, and Norad systems.

Receiver Independent Exchange (RINEX) Format Navigation File

A RINEX Navigation File is an ASCII file of GPS Broadcast Ephemeris data conforming to the RINEX standard. RinexNavFiles (also known as GPS Broadcast Ephemerides) contain position, velocity, and clock information for all the satellites of the GPS constellation. FreeFlyer has the ability to read and write RinexNavFiles, but does not generate Broadcast Ephemeris data when propagating spacecraft. The time system is GPS Time, and positions and velocities are in the ECEF reference frame, which FreeFlyer converts into the ICRF frame. More information on the RINEX format can be found in several locations. Two example references are provided below:

Receiver Independent Exchange (RINEX) Format Observation File

A RINEX Observation File is an ASCII file of Pseudorange data conforming to the RINEX standard. The time system is GPS Time, and the scalar data is reference frame independent. More information on the RINEX format can be found in several locations. Two example references are provided below:

Radius

Distance from the orbit focus to the spacecraft. State vector element in the Spherical and Spherical Lat/Long systems.

Range

The distance between two Spacecraft or from a Spacecraft to a GroundStation. See related methods: Spacecraft.CloseApproachRange, Spacecraft.TCA, GroundStation.Range, Spacecraft.Range.

Runge-Kutta (RK)

A family of Runge Kutta integrators is available in FreeFlyer. The Runge Kutta integration methods are very robust and are ideal for general orbit propagation and for use with impulsive and finite maneuvers. See also Spacecraft Propagators or Spacecraft Motion Modeling.

Satellite Tool Kit (STK) Ephemeris File

The STK® Ephemeris File is an ephemeris-file format that can be used for both input and output of Spacecraft orbital data. The STK Ephemeris allows you to store the state of the Spacecraft at each time step during the mission to a file. When the data is stored in a file, FreeFlyer or Analytical Graphics' Satellite Tool Kit can import the data and perform calculations on the trajectory information. See the Working with Ephemerides guide for more information about creating and importing an Ephemeris file.

Satellite Tool Kit (STK) Attitude History File

The STK® Attitude History File (AHF) is an ephemeris-file format for use with Analytical Graphics Inc.’s Satellite Tool Kit®. This format can be used with FreeFlyer for input of Spacecraft attitude data.

Schatten Solar Flux Prediction Files

The Schatten solar flux prediction files (epochs, geomagnetic indices and exospheric temperatures) can also be used in conjunction with modeling the atmospheric drag forces in the software. The Schatten predicted Jacchia-Roberts files provide predicted monthly mean smoothed estimates of future solar radiation along with weighted planetary geomagnetic index (Ap) to produce atmospheric density values. The Schatten files model three flux magnitude variations (plus two sigma, mean, minus two sigma low), and three phasings (early, nominal, late) of the solar cycle predictions. See also Schatten Solar Flux Files.

Semimajor Axis (a, A, SMA)

The mean distance between apoapsis and periapsis in an elliptical orbit or half of the distance between apoapsis and periapsis, represented as a or A in the Keplerian, Nonsingular Keplerian, Equinoctial, Brouwer-Lyddane Mean, and J2 Brouwer-Lyddane coordinate systems. See related property: Spacecraft.A.

Smoother

A set of algorithms designed to "smooth" state estimates provided by a filter. In FreeFlyer, the Smoother object contains algorithms to smooth the orbit states provided by the Kalman filter over a user-defined interval. The Smoother is accessed via the KalmanFilterOD and UnscentedKalmanFilterOD objects. See the Orbit Determination guide for information on setting up a Kalman Smoother and using the Smoother.

Solid Tides

FreeFlyer uses the Solid Tides Love Number file (IERS2003.dat) to model the effects of Solid Tides. The Solid Tides file contains data used for modeling the Earth's solid-tides induced by perturbing bodies (primarily the Sun and Moon). The data is taken from the IERS Technical Note 32, published in 2003. This data primarily consists of the Love Numbers for Earth, up to Degree and Order 3. Additionally, the file contains coefficients (A0 and H0) used for modeling the Permanent Tide contribution for Earth. These coefficients are used in conjunction with a Tide-Free geopotential, such as the EGM-96. The other geopotential files included with FreeFlyer (JGM-2, GGMO2C) are Zero-Tide models, and already have the Permanent Tide contribution included in the J2 term. See the Solid Tides section of the Spacecraft Force Model guide for more information on implementation.

South Atlantic Anomaly (SAA)

The Earth is surrounded by a pair of concentric donut-shaped clouds called the Van Allen radiation belts which store and trap charged particles from the solar wind. Above South America, about 200 - 300 kilometers off the coast of Brazil, and extending over much of South America, the nearby portion of the Van Allen belt forms what is called the South Atlantic Anomaly. Satellites and other spacecraft passing through this region of space actually enter the Van Allen radiation belt. This can produce 'glitches' in astronomical data, problems with the operation of on-board electronic systems, and premature aging of computer, detector, and other spacecraft components. FreeFlyer includes SAA Regions as Object Presets as well as ISS Over SAA and SAA Sample Mission Plans as examples of implementation.

Spherical Elements

An element set to define the spacecraft location in terms of a coordinate system, mapped on a sphere. The position of the satellite against the sphere is determined by two angles, the right ascension and declination, and the radius vector of the satellite. The velocity of the satellite is given by the speed of the satellite and two angles, the flight path angle and the azimuth of the velocity. The input/output Spacecraft object properties for this set are: SphericalRadius, RA, DEC, Vi, SphericalAzimuth, VerticalFPA. See the Orbit Element Types page for more information.

Spherical Lat/Long

These elements are a variation of the spherical elements. This combines the Earth fixed latitude and longitude properties with inertial velocity properties. This element type is also known as geographic elements. The input/output Spacecraft object properties for this set are: LatLongRadius, Latitude, Longitude, LatLongVi, LatLongAzimuth, HorizontalFPA. See the Orbit Element Types page for more information.

Spacecraft Planet Instrument C-Matrix Events (SPICE) Files

SPICE files are ephemerides created and maintained by the Navigation and Ancillary Information Facility (NAIF) Node of the Planetary Data System. SPICE ephemerides can be used to define the motion of Spacecraft or Celestial Objects in FreeFlyer. SPK files are an element of the SPICE system. They are binary files which may be smoothly interpolated to retrieve an object's position and velocity at any instant within the file time-span. SPK stands for "Spacecraft and Planet Kernel". SPK files may hold ephemerides for any kind of spacecraft, vehicle or solar system body. These SPK files (with the extension .bsp) are the files used by FreeFlyer when propagating Spacecraft or Celestial Objects using SPICE data. For information about using SPICE ephemerides with Spacecraft objects, see the Using a SPICE Ephemeris page of the Spacecraft Propagation guide. For information about using SPICE ephemerides with Celestial Objects, see the Celestial Objects page of the Interplanetary Analysis guide.

Standard Product 3 (SP3) Ephemeris File

An SP3 ephemeris file (also known as "Precise Ephemeris") is an ASCII file of Precise Ephemeris SP3 files conforming to the Ephemeris SP3 standard. SP3 ephemeris files contain data records for the orbit and clock states for the entire GPS constellation. There are two versions of the format, Version A and Version C. FreeFlyer has the ability to read and write both versions. The data records are nominally provided at 15 minute intervals, the time system of the file is GPS time, and the reference frame for the orbit data is Earth-Centered-Earth-Fixed (ECEF). FreeFlyer automatically converts between ECEF and ICRF when reading and writing SP3EphemerisFiles. More information on the SP3 format can be found in several locations. Two example references are provided below:

Structured Query Language (SQL)

SQL provides connectivity between FreeFlyer and Database Management Systems (DBMS). See the Databases page of the Interfacing with External Resources guide for more information.

Sun-synchronous Orbit

A sun-synchronous orbit allows the spacecraft to pass over the same point on the Earth at approximately the same local time each orbit. The orbit is circular, inclined at ~98 with an RAAN of 279.4. The orbit precesses at a rate equal to the Earth's motion around the sun. FreeFlyer includes an Orbit Wizard that allows you to easily create sun-synchronous orbits. The equations used to set this Orbit Type are:

Solve for Inclination:

Given altitude (hp) A = RE + hp

Inclination:

Solve for Altitude: Given Inclination (I):

Altitude:

Where:

•μ = 398600.5

•Ωdot = 360 deg

•Ωdot = 1.99102128e-7 rad/sec

•RE = Radius of the Earth = 6378.136 km

•J2 = 1082.3 x 10-6

Time of Periapsis Passage

Time when the satellite passes through the point of periapsis. See related Spacecraft object properties: OrbitPeriapsis, OrbitPerigee, OrbitPeriselene.

TRK-2-34 Observation File

The TRK-2-34 is a binary file format for DSN data. FreeFlyer extracts sequential range data (SRA), Total Count Phase (TCP) data, and frequency ramping data. FreeFlyer internally converts the ambiguous sequential range data (in Range Units) to DSNObservation.Range measurements (in km) and Total Count Phase (in counts) to DSNObservation.RangeRate measurements (in km/s) using the frequency ramp tables. The format for this data type is specified in the JPL document "TRK-2-34 DSN Tracking System Data Archival Format", Revision O, October 2015. See the Tracking Data File Formats guide for more information.

Trajectory Node

Representation of an individual node point within a TrajectoryPhase object. Nodes represent the discretized path of the TrajectoryPhase.

Trajectory Phase

Representation of a user configurable trajectory arc for solving generic optimal control problems in FreeFlyer. Users can configure and link multiple trajectory phases with varying control models including: ballistic, simple thruster, and ideal solar sail control models. Using the TrajectoryPhase object, users can add bounds and constraints to the optimization problem to reflect real world limits when optimizing the objective function.

True Anomaly (TA, θ)

True Anomaly (TA) is the angle at the focus between the periapsis radius and the radius vector drawn from the focus to the orbiting body. See related property: Spacecraft.TA. Element in the Keplerian system state vector.

True Equator Mean Equinox (TEME)

The X and Z axes point toward the mean vernal equinox and true rotation axis at the current point in time (updated as the spacecraft moves in its orbit). See Orbit Reference Frames.

True-of-Date (TOD) Earth Fixed Coordinate System

The z-axis is the north-pointing vector normal to the true equatorial plane at the current time. The x-axis is the vector from the center of the Earth to the intersection of the prime meridian with the true equatorial plane. The y-axis is the vector perpendicular to the x- and z- axes, which forms a right-handed coordinate system. The true of date Earth fixed coordinate system is time dependent. The origin of the coordinate system is set at the center of the Earth. See the appropriate section of the orbit reference frame page for more information.

True-of-Date (TOD) Earth Equator Coordinate System

The z-axis is the north-pointing vector normal to the true equatorial plane at the current time. The x-axis is the vector from the center of the Earth to the true vernal equinox at the current time. The y-axis is the vector perpendicular to the x- and z- axes which forms a right-handed coordinate system. The true of date Earth equator coordinate system is time dependent – the directions of the coordinate system axes change slightly with time. The origin of the coordinate system is the center of the Earth. See the appropriate section of the orbit reference frame page for more information.

Umbra

The inner part of a conical shadow, which is the darkest, central part, where the light is totally excluded. See related method: Spacecraft.UmbralShadowTimes.

Universal Time (UT1)

A non-uniform time based on the Earth’s rotation, measured as the precise angular coordinate of the Earth about its spin axis. See the Epoch Systems table in the Parsing Dates and Times guide.

Universal Tracking Data Format (UTDF) File

UTDF files contain GroundStation Observation data (azimuth, elevation, range, range rate) from 75-byte binary files written in the Universal Tracking Data Format (UTDF). The time system is UTC, and the angle data is given as azimuth and elevation in GS Local coordinates. UTDF, Bilateration Ranging Transponder System (BRTS) UTDF, and Tracking Data Relay System (TDRS) UTDF are binary 75 byte formats described in detail in the GSFC document "Tracking And Acquisition Handbook For The Spaceflight Tracking And Data Network", October 1994.

UVW Spacecraft Attitude Reference Frame

The UVW coordinate system is quasi-inertial, in the sense that it is treated as an inertial coordinate system (for example, for the purpose of velocity conversions), but it is redefined at each point of interest. The x-axis is the vector pointing in the direction of the Spacecraft's velocity, the y-axis is the vector pointing in the direction normal to the orbit, the z-axis is the vector perpendicular to the y- and z-axes, forming a right-handed coordinate system, and the origin is located at the center of the Spacecraft. See the appropriate section of the attitude reference frame page for more information.

Velocity-Normal-Binormal (VNB) Spacecraft Attitude Reference Frame

The origin of the VNB coordinate system is the center of the Spacecraft. The x axis is in the direction of the Spacecraft’s velocity. The y axis is normal to the orbit plane (the orbit normal being in the direction of the vector product r x v). The z axis forms a right-handed coordinate system. See the appropriate section of the attitude reference frames page for more information.

Vertical Flight Path Angle (VFPA)

Complement to the HFPA, the VFPA is the angle between the velocity vector and the spacecraft position vector. This is an element in the Spherical system state vector.

World Geodetic System (WGS) 1984 Spheroid

World Geodetic System, a reference Earth spheroid. See related methods: GroundStation.Elevation, GroundStation.ElevationR, VisibilitySegment.CalculateRefraction.