The FreeFlyer Target command begins a block of commands, called a targeting loop, that attempts to Achieve a desired set of goals by Varying the values of a user-specified set of input properties. The targeting loop solves a Two-Point Boundary Value Problem (TBVP) using the differential corrector method. The differential corrector uses seed values for the input properties to determine the output values for other properties. It then compares the output to the desired goals, adjusts the input, and iterates the targeting loop until the output is within the specified tolerance.
A differential corrector process consists of first making small variations or perturbations to input properties. The resulting changes in the outputs are measured to determine the relationship to the changes in the inputs. These changes are referred to as the sensitivity matrix (i.e. the Jacobian matrix). In a process that uses the inverse of the sensitivity matrix, the input properties are tuned so that the outputs move closer to the goals. This method usually requires several iterations to reach the goals. Its ability to find a solution that converges, or meets the goals within a defined tolerance, depends on the sensitivity matrix's capability to be inverted.
Differential correction is best suited for problems in which there are the same number of input and output properties and in which all input properties are independent. This method can also accommodate problems in which there are a different number of input and output properties, using the Moore-Penrose pseudo-inverse. As in all iterative processes, targeting via differential correction is not always guaranteed to converge, and in cases where it fails, the TBVP as posed usually lacks a solution. By default, FreeFlyer's targeter will exit after 35 iterations if a solution has not yet been found.
There are a variety of Sample Mission Plans (included with your FreeFlyer installation) that demonstrate various applications of these topics. Continue to the Maneuvering and Targeting Samples page to view descriptions and images of these examples or jump to one of the Mission Plans listed below.
|
Targeting Algorithm
The targeting "shooting method" works by finding the value of the item to achieve at the initial value of the item to vary. Next, the value of the item to achieve at the perturbed value of the item to vary is found. The next guess is calculated by using the slope of the line formed by the initial and perturbed values to find the intersection of the goal value for the item to achieve. The process is repeated until the achieved value is within a specified tolerance. A one-dimensional case (one vary, one achieve) is shown in the diagram below.
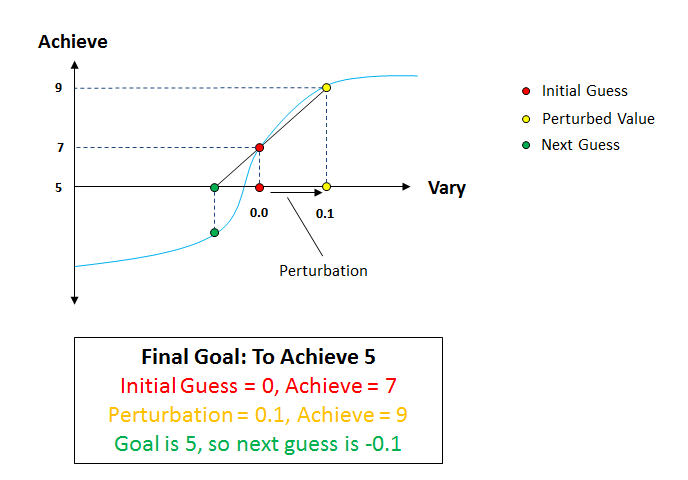
One-dimensional case of the shooting method
Once the targeting process has converged, the Targeter executes a final pass using the converged solution. The DifferentialCorrector.Converged and DifferentialCorrector.IterationMode properties can be used to detect whether the Targeter is executing this final pass. If desired, users can build logic based around these properties to generate visualizations only for the converged solution rather than for every iteration of the targeting process.
Components of a Targeting Loop
Target; Iterate Spacecraft1; Vary ImpulsiveBurn1.BurnDirection[0] = 0.1 + 0.001; Maneuver Spacecraft1 using ImpulsiveBurn1; Achieve Spacecraft1.Apoapsis = 8000 +/- 10; End; |
•The Target command begins the targeting loop. •The Iterate command specifies the objects that are restored to their initial states at the beginning of each iteration of the loop. If it is the first nominal iteration, the Iterate command saves the state of the iterated object. Otherwise, the Iterate command restores the state of the iterated object. •The Vary command defines the object properties that are adjusted. The amount the object property is varied can be constrained by providing a minimum and a maximum. On the first nominal iteration, the Vary command tells the differential corrector current value of the seed expression. On nominal iterations other than the first, the Vary command tells the differential corrector the current value of the perturbation and constraint expressions and sets the varied expression to the value determined by the differential corrector (either nominal or perturbed value). •A process is carried out on the Iterated and Varied objects, such as a Maneuver or Step. •The Achieve command defines the goals of the targeting sequence. The Achieve command tells the differential corrector the current value of the expression being achieved. If it is a nominal iteration, the Achieve command tells the differential corrector the current value of the target and tolerance values. •The Targeter allows users to put Iterate, Vary, and Achieve commands inside loops (If, While, For, etc). The number and type of items being targeted do not need to be known at the time the script is written, allowing the user to load targeting parameters from a file or database at runtime. •When defining a Vary after an Achieve, its partial with respect to that Achieve will automatically be set to zero. •An End statement closes the targeting loop. •A DifferentialCorrector object can optionally be used to set the maximum number of iterations allowed and provides access to the status of the Targeting loop. •The ResetTargetingLoop command is an optional component of the Targeting loop which allows the user to re-initialize the seeds and perturbations to the Vary command if the Targeting process is not converging properly. •Properties and Methods with a state are always reset at the start of each iteration of a Target loop. |
Targeting in Millisecond Precision Mode
FreeFlyer contains two separate timing precision modes, and the Targeter behaves slightly differently in each timing precision mode. As of FreeFlyer 7.3, the default timing precision mode is nanosecond precision mode.
In millisecond precision mode, the Target command keywords "with RuntimeSetup" can be used in order to match the Targeter behavior to the nanosecond precision mode behavior described above. If the "with RuntimeSetup" keywords are not used, then Iterate, Vary, and Achieve commands can not be used inside loops (If, While, For, etc), and all Vary commands must be before all Achieve commands. This means that the number and type of items being targeted must be known and hard-coded at the time the script is written.
![]() Details on Targeting in millisecond precision mode without the RuntimeSetup keyword
Details on Targeting in millisecond precision mode without the RuntimeSetup keyword
•The Target command begins the targeting loop. When the Target loop is entered, the seed value for each Vary is obtained, and the state of each iterated object is saved. •The Iterate command specifies the objects that are restored to their initial states at the beginning of each iteration of the loop. The Iterate command does not result in any execution. •The Vary command defines the object properties that are adjusted. The amount the object property is varied can be constrained by providing a minimum and a maximum. The vary command executes constraints on the guess values calculated in the target command and assigns it to the specific variable or property. •A process is carried out on the Iterated and Varied objects, such as a Maneuver or Step. •The Achieve command defines the goals of the targeting sequence. The Achieve command retrieves the achieved value, goal value, and the tolerance value. •An End statement closes the targeting loop. •A DifferentialCorrector object can optionally be used to set the maximum number of iterations allowed and provides access to the status of the Targeting loop. •The ResetTargetingLoop command is an optional component of the Targeting loop which allows the user to re-initialize the seeds and perturbations to the Vary command if the Targeting process is not converging properly. •Properties and Methods with a state are always reset at the start of each iteration of a Target loop. |
Note: There are several other differences between the nanosecond and millisecond modes. See the timing precision mode page for more information.
See Also
|
•Target Command •Iterate Command •Vary Command •Achieve Command •Maneuver Command •ResetTargetingLoop Command |