The attitude system specifies the method FreeFlyer uses to orient a Spacecraft object with respect to the chosen attitude reference frame. As part of this, Spacecraft attitude can be set using a custom CoordinateSystem object using the Spacecraft.SetOrientation() and Spacecraft.SetAttitudeRefFrame() methods as described in the Vectors and Coordinate Systems guide. The attitude systems available in FreeFlyer are as follows.
Euler Angles
An Euler Angle attitude system consists of an Euler Sequence, the Euler angles, and Euler angle rates. Any orientation can be converted to any other orientation through a maximum of three rotations about the specified axes. The image below shows an example of the use of Euler angles to reorient an object.
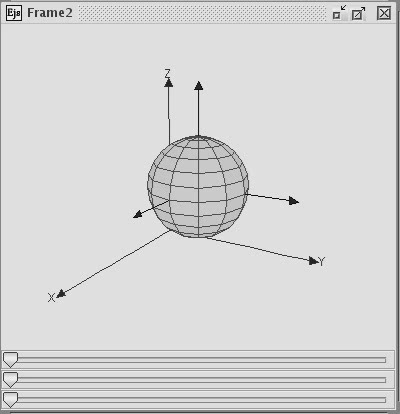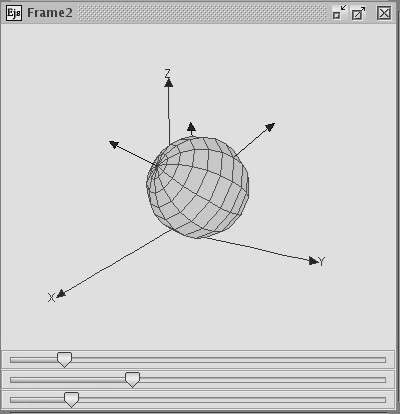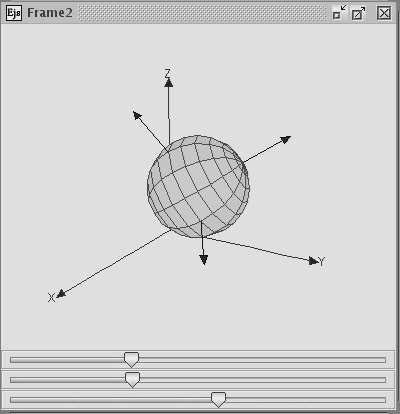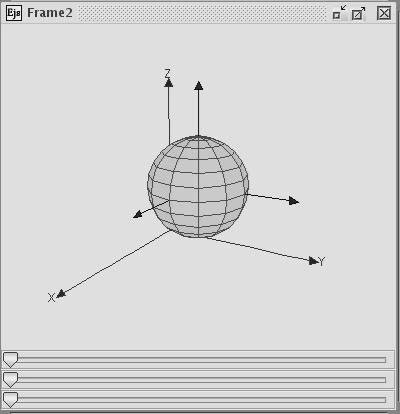
Euler Sequence
The Euler sequence specifies the sequence of axes about which the Euler angles will be applied. There are twelve possible Euler sequences, such as "1-2-3", as shown in the table below.
Rotation Sequence |
Rotation #1 |
Rotation #2 |
Rotation #3 |
1-2-3 |
X-axis |
Y-axis |
Z-axis |
1-3-2 |
X-axis |
Z-axis |
Y-axis |
1-2-1 |
X-axis |
Y-axis |
X-axis |
1-3-1 |
X-axis |
Z-axis |
X-axis |
2-1-3 |
Y-axis |
X-axis |
Z-axis |
2-3-1 |
Y-axis |
Z-axis |
X-axis |
2-1-2 |
Y-axis |
X-axis |
Y-axis |
2-3-2 |
Y-axis |
Z-axis |
Y-axis |
3-1-2 |
Z-axis |
X-axis |
Y-axis |
3-2-1 |
Z-axis |
Y-axis |
X-axis |
3-1-3 |
Z-axis |
X-axis |
Z-axis |
3-2-3 |
Z-axis |
Y-axis |
Z-axis |
The equation below shows how FreeFlyer would apply a 1-2-3 Euler sequence with Euler angles of a1, a2, a3. This shows how the first rotation (which will be about the x-axis in this example) is applied first via the rightmost matrix, followed by the second rotation about the y-axis, and finally the third rotation about the z-axis is applied using the leftmost matrix. This example assumes that the Spacecraft's attitude reference frame is "LVLH", as indicated by the input "LVLHVector". The output vector is in the Spacecraft BCS frame. Additional input frame options are ICRF or geodetic.
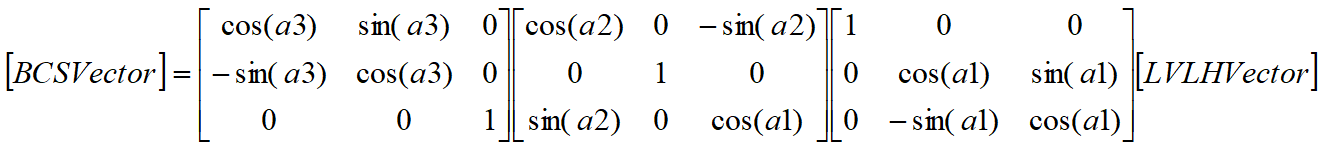
To set the Euler sequence in FreeFlyer script, the Spacecraft.EulerSequence property is used.
Spacecraft1.AttitudeSystem = "EulerAngles"; Spacecraft1.AttitudeRefFrame = "LVLH";
// Set the Spacecraft's Euler Sequence to 3-1-3 Spacecraft1.EulerSequence = {3, 1, 3}; |
Euler Angles
The Euler angle defines the angle the frame is rotated around the specified axis. For instance, with an Euler Sequence of "3-1-3" as set above, the first Euler Angle is a rotation about the z-axis, the second rotation is about the x-axis, and the final rotation is about the new z-axis. Note that Euler angle 1 is applied to the axis specified by the 1st component of the Euler sequence (in this case, the z-axis) and that this is not necessarily the x-axis. To set the Euler angles in FreeFlyer script, the Spacecraft.EulerAngles property is used as follows.
// 30-degree rotation about the 1st axis (specified by EulerSequence[0]) // 45-degree rotation about the 2nd axis (specified by EulerSequence[1]) // 5-degree rotation about the 3rd axis (specified by EulerSequence[2]) Spacecraft1.EulerAngles = {30, 45, 5}; |
When reporting orientations in Euler angles, FreeFlyer constrains the value of the second angle based on the Euler Sequence to resolve ambiguities. For symmetric Euler Sequences (for example, 3-1-3), the second angle will be constrained between 0 and 180 degrees. For asymmetric sequences (for example, 3-1-2), the second angle will be constrained between -90 and 90 degrees. Note that when reporting the Spacecraft.EulerAngles property, all values are represented between 0 and 360 degrees, so the second angle will be reported between 0 and 90 degrees or 270 and 360 degrees. If a user directly assigns the second angle outside of the constraint ranges, the Spacecraft.EulerAngles property will retain the user-specified value until another operation is applied to the Spacecraft attitude, at which point the angles will be represented with the appropriate constraint applied. These constraints are in keeping with the convention defined in the text "Spacecraft Attitude Determination and Control" by James R. Wertz.
Note: Euler angles can be referenced to a custom CoordinateSystem object.
Euler Angle Rates
The Euler rate defines the rate at which the corresponding Euler angle is changing. The Euler angles will be updated based on the value of the corresponding rates whenever the Spacecraft is propagated using the Step or Maneuver commands. To set the Euler rates in FreeFlyer script, the Spacecraft.EulerRates property is used:
// The 1st Euler Angle is not changing with time // The 2nd Euler Angle is changing at a rate of 0.1 degrees per second // The 3rd Euler Angle is changing at a rate of 2 degrees per second Spacecraft1.EulerRates = {0, 0.1, 2}; |
Quaternions
The quaternion attitude system consists of a hyper-complex number, the elements of which can be used to calculate the components of a vector representing an axis of rotation and an angle to be rotated about that axis. The rotation is done using the right-handed convention and the last component represents the scalar element. This is in keeping with Euler's theorem that any orientation can be achieved from any other orientation with a single rotation about a single axis, which may or may not be one of the reference frame chief axes. The quaternion elements used in FreeFlyer, as represented in the following equation, are [Q1, Q2, Q3, Q4] where Q12 + Q22 + Q32 + Q42 = 1. Quaternions in FreeFlyer are defined based on the text "Spacecraft Attitude Determination and Control" by James R. Wertz.
|
To set the Spacecraft.Quaternion array in FreeFlyer script, the following syntax is used.
Spacecraft1.AttitudeSystem = "Quaternion"; Spacecraft1.Quaternion = {0, 0, 0, 1}; |
The angular velocities associated with the quaternions are controlled using the Spacecraft.AngularVelocity property, meanwhile angular acceleration values can be viewed with the Spacecraft.AngularAcceleration property.
Spacecraft1.AngularVelocity = {0, 0, 0};
Report Spacecraft1.AngularAcceleration; |
The following example shows how to multiply two quaternions representing 90° rotations about the +X and +Y axes.
// Define two quaternions (q1 and q2) Array q1 = {0.7071, 0.0, 0.0, 0.7071}; // 90° rotation about +X Array q2 = {0.0, 0.7071, 0.0, 0.7071}; // 90° rotation about +Y
// Assign q1 to the spacecraft's attitude quaternion Spacecraft s; s.Quaternion = q1;
// Multiply the spacecraft quaternion (q1) by q2 Array qProduct; qProduct = s.Quaternion.QuaternionMultiply(q2);
// Report results Report q1; Report q2; Report qProduct; |
The result, [0.5, 0.5, 0.5, 0.5], corresponds to a single 120° right‑handed rotation about the (1,1,1) axis.
Note: The Quaternion attitude system can be referenced to a custom CoordinateSystem object.
Attitude Matrix
The attitude matrix allows the user to define a Spacecraft's attitude with respect to its attitude reference frame using a 3x3 matrix. This matrix is orthogonal, its determinant should equal 1, and when multiplied by its transpose should result in the identity matrix. In FreeFlyer script, the Spacecraft.AttitudeMatrix property is used to set the attitude matrix as demonstrated in the following example.
Spacecraft1.AttitudeSystem = "AttitudeMatrix";
Spacecraft1.AttitudeMatrix = [1, 0, 0; 0, 1, 0; 0, 0, 1]; |
Note: The attitude matrix can be referenced to a custom CoordinateSystem object.
Spinner
The spinner attitude system defines a Spacecraft which rotates about its angular momentum vector, which is then defined as the Spacecraft's z-axis. The following properties can be manipulated to set up a spinner system.
Angular Momentum Vector
•Right Ascension oDefines the right ascension of the Spacecraft's angular momentum vector in the ICRF inertial frame •Declination oDefines the declination of the Spacecraft's angular momentum vector in the ICRF inertial frame |
Spacecraft1.AttitudeSystem = "Spinner";
Spacecraft1.AngularMomentumRightAscension = 90; Spacecraft1.AngularMomentumDeclination = 0; |
Spin Rate
•Nutation Angle oDefines the coelevation of a spinning Spacecraft's spin axis with respect to the z-axis of the angular momentum frame oNutation is ignored for spherical spacecraft •Spin Axis Coelevation oDefines the initial right ascension of a spinning Spacecraft's spin axis with respect to the angular momentum frame •Spin Rate oDefines the angular rotation rate of a spinning Spacecraft about its spin axis •Phase Angle oDefines the phase angle of the x-axis of the BCS with respect to the projection of the x-axis of the GCI into the spin plane |
Spacecraft1.NutationAngle = 0; Spacecraft1.CoElevation = 0; Spacecraft1.SpinRate = 0; Spacecraft1.SpinPhase = 0; |
See Also