To begin configuring a Batch Least Squares estimation process in FreeFlyer, add a BatchLeastSquaresOD object to your Mission Plan using the Object Browser. After double-clicking on the new object, you will see the "Estimation Model" page of its object editor. From this page, you can set initial options, such as the maximum allowable residual sigma, the solution epoch, and whether or not to constrain the data span to a specified start and end epoch.
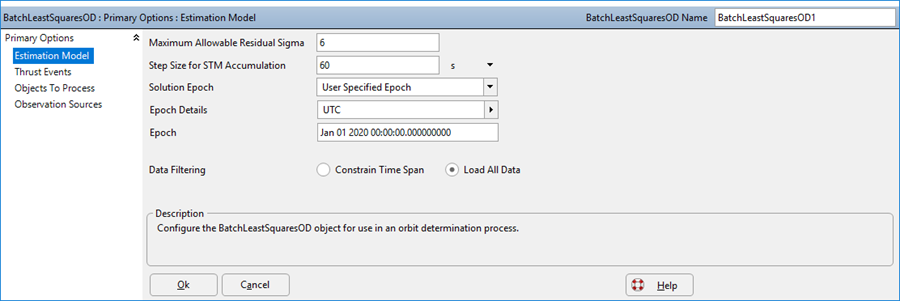
Estimation Model Page for the Batch Least Squares OD Object Editor
You can also create and configure a BatchLeastSquaresOD object through FreeFlyer script. Some BatchLeastSquaresOD properties and methods are only accessible through FreeFlyer script. The AprioriCovarianceOption and MeasurementEditingOption properties are two examples.
The AprioriCovarianceOption property lets you choose one of four different approaches to handling the a priori covariance in the Batch Least Squares OD process:
•Use the user-specified covariance for all properties in the state vector. •Don't seed the a priori state covariance at the start of each iteration. This affectively sets the inverse of the covariance to zero. •Ignore the a priori covariance for the initial iteration of the batch, and use the post-update computed covariance for subsequent iterations. •Compute the optimal a priori covariance for each iteration of the batch.
Note: The last option uses the measurement information matrix in order to compute the a priori covariance for each Batch Iteration. |
The MeasurementEditingOption property lets you choose one of two different methods for performing measurement editing: use the predicted RMS to edit data, or use the standard deviation to edit data. Data is edited based on the MaxAllowableSigma property, depending on what the MeasurementEditingOption property is set to use. Using the predicted RMS to edit data tends to edit more data than when using the standard deviation, because it is more sensitive to a poor a priori state.
The syntax example below shows how to create a BatchLeastSquaresOD object and set its initial options.
// Create and set up Batch BatchLeastSquaresOD BatchLeastSquaresOD1;
BatchLeastSquaresOD1.AprioriCovarianceOption = 0; // Corresponds to "Use the user-specified covariance for all properties in the state vector." BatchLeastSquaresOD1.MeasurementEditingOption = 0; // Corresponds to "Use the predicted RMS to edit data" BatchLeastSquaresOD1.MaxAllowableSigma = 6; // Sigma reference depends on the Measurement Editing Option BatchLeastSquaresOD1.SolutionEpochOption = 0; // Corresponds to "Beginning of Arc" BatchLeastSquaresOD1.SolutionDampingOption = 0; // Corresponds to "Do not use Solution Damping" |
Once this initial setup is complete, continue configuring your OD system by:
•Defining the A Priori States •Defining the Measurement Model •Defining Thrust Events •Defining the Properties to Estimate •Including Tracking Data |
Solution Epoch
The options for the solution epoch are:
•Beginning of Arc •Middle of Arc •End of Arc •User-Specified Epoch |
When choosing the Solution Epoch, it is important to consider the time separation between the epoch of the Apriori State and the Solution Epoch. The greater the time difference, the greater the initial Covariance should be.
Epoch Details
Use the Epoch Details editor to define the User-Specified Epoch. See Parsing Dates and Times for more information on working with the Epoch Details editor.
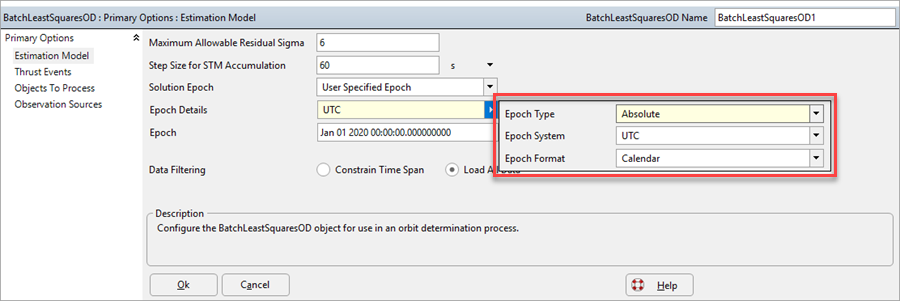
Epoch Details Editor for the Batch Least Squares OD Object Editor
Solution Damping
Solution damping is used in scenarios where Batch Least Squares solutions are prone to divergence (low observability, short-arc, etc.). Solution damping can ensure convergence, but for well-behaved solutions, can actually slow convergence by requiring more iterations. Therefore solution damping is only recommended for cases prone to divergence. There are two solution damping options within FreeFlyer when performing Batch Least Squares estimation. By default solution damping is turned off.
•Levenburg-Marquardt Damping •Quadratic Damping |
Both solution damping methods use the SolutionDampingFactor, SolutionDampingRho, and SolutionDampingRhoTolerance in order to improve the convergence of the Batch Least Squares solution. Each solution damping method scales the Damping Factor based off of Rho and RhoTolerance but they scale the Damping Factor differently. A larger Damping Factor corresponds to more damping. See the equation below for how Rho is calculated based on the weighted RMS (chi), state (X), state update (x-hat), Damping Factor (lambda), measurement matrix (H), weighting matrix (R), and measurements vector (y).
|
The Levenburg-Marquardt damping method uses the SolutionDampingFactorDecrease, and SolutionDampingFactorIncrease properties to scale the SolutionDampingFactor based on the SolutionDampingRho and SolutionDampingRhoTolerance properties in order to improve the convergence of the Batch Least Squares solution. Rho is a quality factor to quantify the quality of the state update compared to the pre-state update. A larger Rho corresponds to a higher quality state update. If Rho is large compared to RhoTolerance, the Damping Factor will be scaled down by a factor of FactorDecrease. If Rho is less than the RhoTolerance, the Damping Factor will be scaled up by a factor of FactorIncrease.
The Quadratic damping method is the more robust, but slower method of the two. It uses the SolutionDampingFactor and SolutionDampingAlpha properties based on the SolutionDampingRho and SolutionDampingRhoTolerance properties in order to improve the convergence of the Batch Least Squares solution. Similar to the Levenburg-Marquardt method, the Quadratic damping method uses Rho depending on RhoTolerance to scale the Damping Factor or not. However, the amount the Damping Factor is scaled is determined by Alpha instead of the FactorDecrease and FactorIncrease properties. In the Quadratic damping method the Damping Factor is only scaled if Rho is below RhoTolerance. Below are the equations for calculating Alpha and how Alpha and Rho are used to scale the Damping Factor:
|
Step Size for State Transition Matrix Accumulation
When performing Batch Least Squares estimation, all the observation data must be mapped from the observation epochs to the Solution Epoch; this is accomplished with the State Transition Matrix (STM). FreeFlyer allows the user to choose the Step Size that is used when accumulating the STM between observation epochs.
For each Spacecraft included in the Batch Least Squares estimation process, there are three options for how the STM is calculated. See Spacecraft OD Setup for more information.
1.J2 Semi-analytic – This method uses analytic partial derivatives based on the force model of the Spacecraft. The point-mass of all celestial bodies are included, and the J2 term of the Central Body’s gravity potential is also included. This method is faster but less accurate. This method is a second order approximation that is most accurate at a 16 second step-size.
2.Numeric – This method uses centrally-differenced numeric partial derivatives for all forces included in the force model of the Spacecraft. The STM partials are computed through a forward Euler approximation. This method is more accurate than the J2 Semi-analytic method, but slower. 3.Variational Equations – This method numerically integrates the partial derivatives of the spacecraft accelerations to compute the state transition matrix. Variational Equations is the recommended approach, since this method is faster and more accurate than the Numeric method, and less sensitive to the propagator step size setting. When using the Variational Equations approach for covariance propagation, the partial derivatives of the dynamical model with respect to the estimated state are numerically integrated along with the propagated state. |
See Also
•BatchLeastSquaresOD Properties and Methods |