FreeFlyer's optimization capability can be used to solve a variety of problems related to trajectory design, maneuver planning, and more. Optimization features are available in FreeFlyer's Mission tier (see the Features List for details regarding the differences between the Mission and Engineer tiers).
The following Sample Mission Plans (included with your FreeFlyer installation) demonstrate the use of the Optimizer object:
|
The basic components of an optimization problem workflow are as follows, in order:
The script examples on this page demonstrate how a user might configure a two-burn orbit raise to geosynchronous orbit, for which the optimal solution trajectory is a Hohmann transfer. This page is intended as a basic guide to configuring a user-defined optimization problem; for further customization and more advanced options, see Tuning an Optimizer.
Define the Problem
The first step of any optimization process is to define the problem that must be solved. This involves configuring the state variables, constraints, and (optionally) the objective function.
Configuring State Variables
State variables within an optimization process represent the parameters that will be varied by the Optimizer object in order to find the optimal value of the objective function specified by the user. State variables can be added to the process via the Optimizer.AddStateVariable() or Optimizer.AddStateVariableBlock() methods, which require the user to set a label to be used to identify the variable within the process.
Optimizer opt;
opt.AddStateVariable("dv1"); opt.AddStateVariable("dv2");
// Or
opt.AddStateVariableBlock({"dv1", "dv2"}); |
Once added to a process, the user can configure initial guesses, bounds, scales, and perturbations for each state variable. Supplying the Optimizer object with a good initial guess for the state variables in the problem can greatly improve iteration speeds and increase the likelihood of convergence, while specifying appropriate upper and lower bounds can prevent the Optimizer object from iterating through error cases or unrealistic scenarios. The state variables in an optimization process can be accessed either through the Optimizer.StateVariables Array property or by using the Optimizer.GetStateVariable() method and specifying the desired label. There are a number of overloads available for the Optimizer.AddStateVariable() and Optimizer.AddStateVariableBlock() methods which provide the opportunity to configure all of these settings when adding the variable to the optimization process.
opt.GetStateVariable("dv1").InitialGuess = 1; opt.GetStateVariable("dv1").LowerBound = 0; opt.GetStateVariable("dv1").UpperBound = 5; opt.GetStateVariable("dv1").Scale = 1; opt.GetStateVariable("dv1").Perturbation = 0.01;
opt.GetStateVariable("dv2").InitialGuess = 1; opt.GetStateVariable("dv2").LowerBound = 0; opt.GetStateVariable("dv2").UpperBound = 5; opt.GetStateVariable("dv2").Scale = 1; opt.GetStateVariable("dv2").Perturbation = 0.01;
// Alternatively, use different method overloads to add two OptimizationStateVariables to the Optimizer and simultaneously // configure initial guesses, lower bounds, upper bounds, scales, and perturbations for each opt.AddStateVariable("dv1", 1, 0, 5, 1, 0.01); opt.AddStateVariable("dv2", 1, 0, 5, 1, 0.01); |
Configuring Constraints
Constraints are used in an optimization process to define conditions which must be met in order for a solution produced by the Optimizer object to be considered feasible. Similarly to state variables, constraints can be added to the process via the Optimizer.AddConstraint() or Optimizer.AddConstraintBlock() methods, which require the user to set a label to be used to identify the constraint within the process.
opt.AddConstraint("Periapsis"); opt.AddConstraint("Apoapsis");
// Or
opt.AddConstraintBlock({"Periapsis", "Apoapsis"}); |
Once added to a process, the user can configure bounds for each constraint through the methods shown below. The constraints in an optimization process can be accessed either through the Optimizer.Constraints Array property or by using the Optimizer.GetConstraint() method and specifying the desired label.
•Lower and upper (or "inequality") bounds should be configured for cases where a range of values would be acceptable in the solution oTo configure a one-sided inequality, simply set the lower or upper bound and leave the other bound set to the default value. The default bounds are -1e20 for lower bounds and 1e20 for upper bounds. •Equality bounds should be configured for cases where a condition must be met exactly, within a small tolerance |
In the example below, both approaches are shown; the "Periapsis" and "Apoapsis" constraints can be configured with equality bounds so that their values must be 42164 in order for the solution to be feasible or with upper and lower bounds to allow for a bit more flexibility in the solution. Setting a one-sided inequality bound would allow the constraint to be any value "less than" or "greater than" the bound. There are a number of overloads available for the Optimizer.AddConstraint() and Optimizer.AddConstraintBlock() methods which provide the opportunity to configure all of these settings when adding the constraint to the optimization process.
// Equality Bounds opt.GetConstraint("Periapsis").SetEqualityBounds(42164); opt.GetConstraint("Apoapsis").SetEqualityBounds(42164);
// Lower and Upper Bounds opt.GetConstraint("Periapsis").SetLowerAndUpperBounds(42160, 42168); opt.GetConstraint("Apoapsis").SetLowerAndUpperBounds(42160, 42168);
// One-sided Inequality Bounds opt.GetConstraint("Periapsis").SetLowerBound(42160); opt.GetConstraint("Apoapsis").SetUpperBound(42168);
// Alternatively, use different method overloads to add two OptimizationConstraints to the Optimizer and simultaneously // configure lower and upper bounds for each opt.AddConstraint("Periapsis", 42164, 42164); opt.AddConstraint("Apoapsis", 42164, 42164); |
The Optimizer.AddConstraint() method also provides the capability to set the period of the cyclic behavior. For example, an angular constraint in units of degrees could benefit from using a cyclic range of 360. Similarly, a day of week constraint could benefit from using a cyclic range of 7.
// Configure the cyclic range for angle in degrees opt.AddConstraint("CyclicAngle", 0, 220, 1, 360);
// Configure the cyclic range for day of the week opt.AddConstraint("CyclicDayOfWeek", 2, 5, 1, 7); |
Save Objects to Process
Any objects that will need to be reset to their original state with every iteration of the Optimizer object should be saved to the optimization process with the Optimizer.SaveObjectToProcess() method. For example, if a Spacecraft object is propagated within the optimization evaluation loop, the user can Save its state to the optimization process at the beginning of the simulation and then Restore it to that original state at the beginning of each iteration of the optimization loop using the Optimizer.RestoreObjectsInProcess() method. The method will restore all saved objects to their original state without changing the current state variable values.
opt.SaveObjectToProcess(Spacecraft1); |
Objective Function
The objective function defines the quantity that needs to be minimized or maximized by the Optimizer, and can be any value that can be calculated in FreeFlyer script. In practice, this calculation will be performed inside of the optimization loop as showcased later in this guide. For example, if a user wished to minimize the total delta-v across two ImpulsiveBurns in their analysis, they would define their objective function as follows:
ImpulsiveBurn TransferBurn; ImpulsiveBurn CircularizeBurn;
Variable objective;
// The quantity to be minimized by the Optimizer object will be the total delta-v across two ImpulsiveBurns objective = TransferBurn.BurnDirection.Norm + CircularizeBurn.BurnDirection.Norm; |
Load the Optimization Engine
Once defined, the problem must be loaded into a third-party optimization library. FreeFlyer includes a minimum norm constraint solver and built-in support for Ipopt and NLopt. FreeFlyer also supports SNOPT, but the user must have an SNOPT license and provide the path to the SNOPT shared library file (.dll on Windows, .so on Linux). For more information on each third-party tool, see Optimization Engines. The optimization engine is loaded by calling the LoadEngine() method on the Optimizer object. If called with no arguments, Ipopt will be loaded by default.
opt.LoadEngine(); // Ipopt
opt.LoadEngine(0); // 0 = Ipopt, 1 = SNOPT, 2 = NLopt, 3 = Minimum Norm Constraint Solver |
If using SNOPT, the user must provide the path to their shared library file. The user can specify the shared library file for Ipopt or NLopt as well, if they wish to use their own version of the library instead of the one built in to FreeFlyer.
opt.LoadEngine(1 /* SNOPT */, "mypath/snopt7.dll"); |
Each optimization engine has additional settings specific to each library. The process for accessing these tuning parameters is described on the Optimization Engines page.
Create the Evaluation Loop
The evaluation loop is where the bulk of the analysis happens for any optimization problem. After defining the problem and loading the desired optimization engine, the evaluation loop is used to run each iteration of state variable values through the user's analysis, calculate the current constraints and objective, and run the optimization engine until either an optimal solution is found or the engine exits without converging.
Note: The first 3 iterations of an optimization process are "sampling" iterations and do not update any feasibility information or properties. The sampling is done to determine sparsity of the Jacobian and determine what derivatives the user has provided, if any.
Loop Condition
The optimization process happens within a While loop; the Optimizer object will continue to iterate until the condition in the loop evaluates to false. Two methods on the Optimizer object can be used as the loop condition, depending on the desired behavior: HasNotConverged() or IsRunning(). The Optimizer.HasNotConverged() method will return false only when the process converges on an optimal solution, and will throw an error if the process does not converge. Therefore, this is a good condition in the case where the user would only be satisfied with an optimal solution.
While (opt.HasNotConverged());
// Restore saved objects // Update and retrieve state variables // Perform analysis // Update constraints // Minimize or maximize objective function // Generate reports
End; |
If convergence is not required, the Optimizer.IsRunning() method is a better option; this approach does not require that the optimization process converges, only that it exits. The user can then check the Optimizer.ReturnCode and Optimizer.ReturnString properties to learn about the state of the Optimizer object when it exited; each engine can return a variety of return codes. In some cases, a solution can be useful even if the process does not converge (for example, if a feasible solution was found).
While (opt.IsRunning());
// Restore saved objects // Update and retrieve state variables // Perform analysis // Update constraints // Minimize or maximize objective function // Generate reports
End;
Report opt.ReturnCode, opt.ReturnString, opt.FeasibleSolutionFound(); |
Restore Saved Objects
The first step within the evaluation loop is to restore any objects that have been saved to the process and need to be returned to their initial state for each iteration. Any such objects should be affiliated with the Optimizer object before entering the evaluation loop using the Optimizer.SaveObjectToProcess() method as shown above. When the Optimizer.RestoreObjectsInProcess() method is called, any objects that have been saved to the process will be reset to their initial state.
While (opt.HasNotConverged());
// Restore saved objects opt.RestoreObjectsInProcess();
// Update and retrieve state variables // Perform analysis // Update constraints // Minimize or maximize objective function // Generate reports
End; |
If any properties or methods with a state are used in the computation of any constraints or the objective function, they should also be reset at the beginning of the evaluation loop by calling the ResetMethodStates() method on the appropriate object.
While (opt.HasNotConverged());
// Restore saved objects and reset properties and methods with a state opt.RestoreObjectsInProcess(); Spacecraft1.ResetMethodStates();
// Update and retrieve state variables // Perform analysis // Update constraints // Minimize or maximize objective function // Generate reports
End; |
Update and Retrieve State Variables
At the beginning of each iteration of the evaluation loop, the state variables must be updated using the Optimizer.UpdateStateVariables() method. This method advances all the state variables in the process to the Optimizer object's next guess. These state variable values should then be retrieved using the Optimizer.GetStateVariableValue() method (or the Optimizer.GetStateVariableValues() method, which returns an Array of all state variable values), and assigned to any objects or properties being used for analysis as needed.
While (opt.HasNotConverged());
// Restore saved objects
// Update and retrieve state variables opt.UpdateStateVariables();
TransferBurn.BurnDirection[0] = opt.GetStateVariableValue("dv1"); CircularizeBurn.BurnDirection[0] = opt.GetStateVariableValue("dv2");
// Perform analysis // Update constraints // Minimize or maximize objective function // Generate reports
End; |
Perform Analysis
Once the latest state variable values have been retrieved from the Optimizer object, any analysis that is necessary to calculate the constraints or objective function should be performed. This could include Spacecraft propagation, contact analysis, performing maneuvers, and more. In the example below, two maneuvers are performed to place the Spacecraft in its final orbit, at which point the updated constraints can be defined.
TimeSpan BurnEpoch = Spacecraft1.Epoch;
While (opt.HasNotConverged());
// Restore saved objects // Update and retrieve state variables
// Perform analysis // Perform first burn Maneuver Spacecraft1 using TransferBurn;
// Coast for half an orbit Step Spacecraft1 to (Spacecraft1.Epoch == BurnEpoch + TimeSpan.FromMinutes(Spacecraft1.Period/2));
// Perform second burn Maneuver Spacecraft1 using CircularizeBurn;
// Update constraints // Minimize or maximize objective function // Generate reports
End; |
Update Constraints
Once any necessary analysis has been performed, the resulting constraints must be calculated and fed back into the Optimizer object using the Optimizer.SetConstraintValue() method or the Optimizer.SetConstraintBlockValues() method. In the example below, the constraints are defined by the Spacecraft's periapsis and apoapsis.
While (opt.HasNotConverged());
// Restore saved objects // Update and retrieve state variables // Perform analysis
// Update constraints opt.SetConstraintValue("Periapsis", Spacecraft1.Periapsis); opt.SetConstraintValue("Apoapsis", Spacecraft1.Apoapsis); opt.SetConstraintBlockValues("myConstraint", myArray);
// Minimize or maximize objective function // Generate reports
End; |
Provide Known Derivatives
If desired, the user can provide the optimization engine with any known derivatives of the problem constraints or objective function by populating the Jacobian Matrix and Gradient Array properties of the Optimizer object on every nominal case iteration within the evaluation loop. This is an optional input that can improve performance; see Specifying Known Derivatives for more information.
Minimize or Maximize the Objective Function
The objective function defines the quantity which needs to be minimized or maximized by the Optimizer object in order to produce an optimal solution. The objective function is passed in as an argument to the Optimizer.Minimize() or Optimizer.Maximize() method, and the Optimizer object works to vary the state variable values in order to find the best solution to the objective function that meets the problem's defined constraints. In the example below, the objective function is defined as the sum of the delta-v produced by two maneuvers, and the goal is to minimize that quantity.
Variable objective;
While (opt.HasNotConverged());
// Restore saved objects // Update and retrieve state variables // Perform analysis // Update constraints
// Minimize or maximize objective function objective = CircularizeBurn.BurnDirection.Norm + TransferBurn.BurnDirection.Norm; opt.Minimize(objective);
// Generate reports
End; |
Once the call to Optimizer.Minimize() or Optimizer.Maximize() is implemented, the evaluation loop can be considered complete. The third party optimization system will process the constraint and objective values, and find a new set of state variable values for evaluation, which are retrieved at the beginning of the loop by the Optimizer.UpdateStateVariables() method as shown above. This process will repeat until the evaluation loop exits.
An alternative to minimizing or maximizing an objective function is the Optimizer.SolveConstraints() method, which finds a feasible solution to satisfy the problem constraints without needing to specify an objective function. This approach will allow the Optimizer object to converge on a solution that is feasible, but not necessarily optimal.
opt.SolveConstraints(); |
Generate Output
Data reports and graphical output can be generated within the evaluation loop of an optimization process as well as after converging on a solution and/or exiting the loop. Views, Plots, and Reporting mechanisms all behave the same way within an optimization loop as they do in any other context; FreeFlyer's suite of Optimization Sample Mission Plans contain numerous examples of output generation within an optimization process. There are various convenient properties and methods on the Optimizer object that enable the user to easily retrieve information about the optimization process both during and after iteration. Reports about the optimization process within an evaluation loop should always be generated after the call to Optimizer.Minimize(), Optimizer.Maximize(), or Optimizer.SolveConstraints() to ensure that the most up-to-date values are being reported.
The example below demonstrates how to report the current state variable, constraint, and objective function values, as well as the best state variable, constraint, and objective function values that have been found so far. If a feasible solution has not yet been found, the "best" state variable and constraint Arrays will contain values that represent the nominal point with the lowest infeasibility that has been found so far. The example below uses the Optimizer.OptimizationPhase property to report data only for nominal evaluations, and the Optimizer.FeasibleSolutionFound() method to only report the "best" parameters when a feasible solution has been found.
While (opt.HasNotConverged());
// Restore saved objects // Update and retrieve state variables // Perform analysis // Update constraints // Minimize or maximize objective function
// Generate reports // Report current state variable, constraint, and objective function values on each nominal evaluation If (opt.OptimizationPhase == 1);
Report opt.GetStateVariableValues(), opt.GetConstraintValues(), opt.ObjectiveFunctionValue, opt.IsFeasible();
// Report best solution parameters found so far if a feasible solution has been found If (opt.FeasibleSolutionFound()); Report opt.GetBestStateVariableValues(), opt.GetBestConstraintValues(), opt.GetBestObjectiveFunctionValue(); End;
End;
End; |
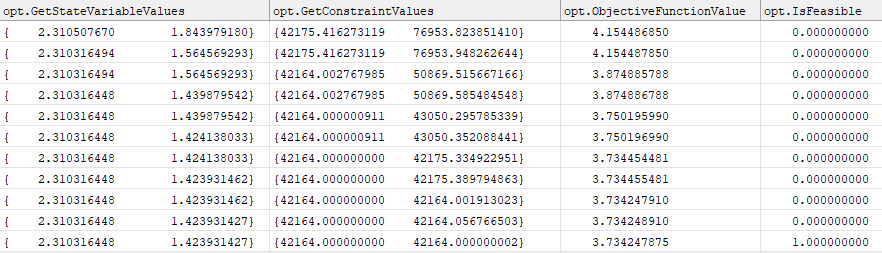
Example output from an optimization process

Example report of best parameters
The standard output from the third-party optimization system can also be retrieved and reported during the optimization process. Reporting the Optimizer.LastGeneratedEngineOutput property to a DataTableWindow or ConsoleWindow allows the user to view a live stream of standard output from the optimization system.
ConsoleWindow optConsole; optConsole.CurrentFontType = 1; // Fixed width font optConsole.Show();
While (opt.HasNotConverged());
// Restore saved objects // Update and retrieve state variables // Perform analysis // Update constraints // Minimize or maximize objective function
// Generate reports // Report engine output If (opt.LastGeneratedEngineOutput.Length != 0); Report opt.LastGeneratedEngineOutput to optConsole; End;
End; |
![]() Example: Ipopt Standard Output in a ConsoleWindow
Example: Ipopt Standard Output in a ConsoleWindow
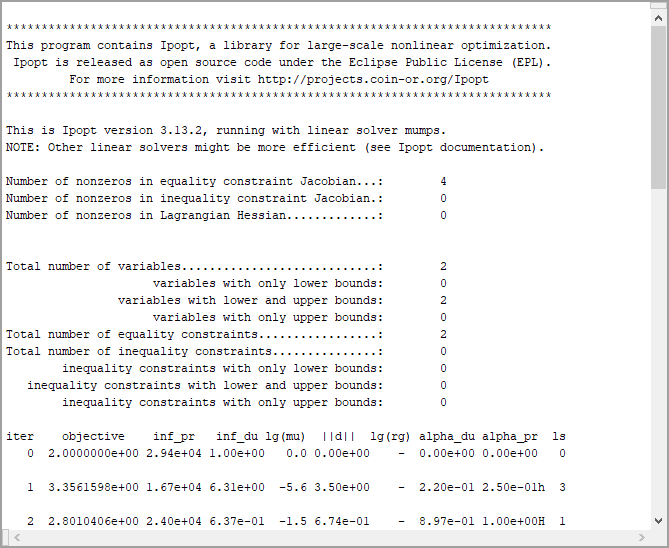 Engine output redirected to a ConsoleWindow |
The Optimization Sample Mission Plans use Procedures to format relevant information from an optimization process in a GridWindow for convenient viewing. The Procedures themselves are located in the "Sample Mission Plans\_Support_Files" directory.
Retrieve the Best Solution
Once the evaluation loop is complete, the user can retrieve the best solution found and use those state variable values to proceed with their analysis. The final evaluation of the Optimizer object is not necessarily the best solution. Once outside of the evaluation loop, it is important to retrieve the best state variable values, rather than just the state variables from the most recent iteration, so that any further analysis will reflect the optimal solution that has been found.
// These will not necessarily be the same Report opt.GetStateVariableValues(); // Most recent evaluation Report opt.GetBestStateVariableValues(); // Best solution - these values should be used to proceed with the analysis |
This concept is demonstrated in the example plot below, where the optimal solution which maximizes the objective function is found before the optimizer exits and is not the final iteration.
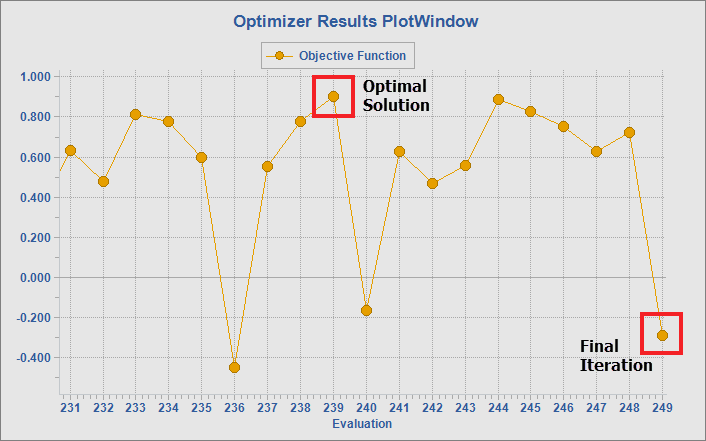
Example Objective Function Plot
Complete Example
The simple example that has been constructed throughout this page is presented in its entirety below, with descriptions to indicate each section of the workflow. The Optimizer object converges on the expected delta-v values for a Hohmann transfer, which is known to be the most efficient solution for a two-burn transfer between two circular orbits.
![]() Example: Hohmann Transfer
Example: Hohmann Transfer
|
This page contains all of the basic components needed to configure a simple optimization problem. For more customization and advanced features, see Tuning an Optimizer, and for more information on the third-party optimization engines, see Optimization Engines.
See Also
•Optimizer Properties and Methods •OptimizationStateVariable Properties and Methods •OptimizationConstraint Properties and Methods |