Is Relative-Only Navigation Plausible for Crewed Missions to NRHOs?
Recently, lunar Near Rectilinear Halo Orbits (NRHO) have been the focus of much study, and they have been selected as the target orbit for the Gateway mission, formerly the Deep Space Gateway. Also, the Deep Space Network (DSN) is increasingly congested and over-subscribed. In this work, the performance of relative-only navigation between a spacecraft in an NRHO and a relay in a Distant Retrograde Orbit is examined and compared to simulated DSN tracking using a Square Root Information Filter. Various tracking scenarios are examined using a closed-loop simulation where navigation errors inform maneuver planning and maneuver execution errors affect navigation performance. Results indicate that relative-only navigation can provide comparable levels of orbit determination error and orbit maintenance costs.
Introduction
Lunar Near Rectilinear Halo Orbits (NRHOs) are currently the primary candidate for the target orbit for the Gateway mission, formerly known as the Deep Space Gateway.1, 2 The NRHO orbit class is selected because it exhibits several useful advantages for human spaceflight.3 These include low orbit maintenance costs, low orbit insertion costs, low orbit transfer costs, and resonant periods that minimize shadowing and communications blockages. Each of these characteristics has been examined in previous works.3-5
Construction and usage of the Gateway, a maneuverable, habitable lunar-orbit staging vehicle for deep space missions, will occur over multiple missions and will contain phases of crewed activity and uncrewed, quiescent operations.6, 7 As such, any orbit maintenance or navigation analysis should incorporate the dynamical disturbances associated with both phases. The uncrewed phase will generally be more quiescent than the crewed phases, as the main orbit disturbances will be momentum unload and orbit maintenance maneuvers (OMM). However, during crewed phases, more orbit disturbances are introduced by the added impacts of human activity. These disturbances are events like CO2 and waste dumps, additional momentum unloads, and attitude slews. These disturbances can be frequent and unplanned, and occur at varying time intervals, making them potentially difficult to model for navigation.
Typically, missions such as Gateway rely on the Deep Space Network (DSN) for tracking; however as of 2015, the DSN supported about 40 deep-space missions and was routinely oversubscribed by about 30%. This demand translates to about 500 hours of over-subscription per week, roughly equivalent to the work of four (4) additional antennas.8 Furthermore, there are currently six (6) more missions to Mars (comprising nine (9) spacecraft) planned for the 2020 launch window, creating an unprecedented level of demand.9 In an attempt to alleviate the expected congestion, the DSN has implemented the Multiple Spacecraft Per Antenna (MSPA) technique, allowing for shared antenna time. However, this is restricted to spacecraft within the same beam-width and all secondary spacecraft are limited to downlink only.10
Given this over-subscription, it makes sense to investigate alternative navigation strategies that might alleviate these scheduling constraints. Relative navigation approaches in cis-lunar space have been investigated previously, and they have demonstrated suitable navigation accuracies for robotic missions.11-13 In addition, NASA has contracted for additional studies on technologies related to peer-to-peer navigation in cis-lunar space.14 The previous works typically considered the combination of low-lunar orbit and Halo obits for the relative navigation scenario. This analysis considers relative navigation between an NRHO and a DRO.
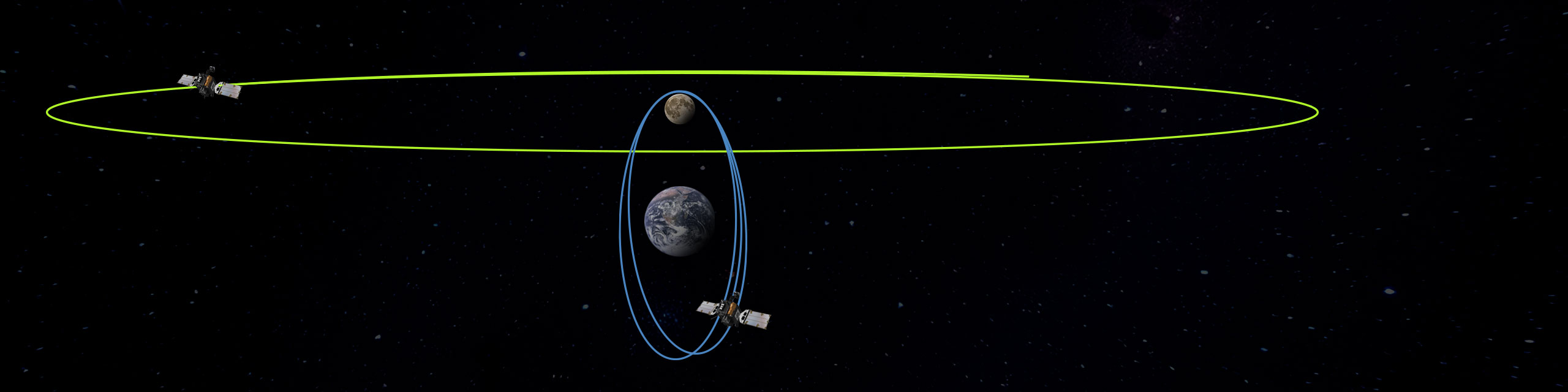
The orbit chosen for the Gateway is an L2 Southern NRHO with an average periapsis altitude of approximately 1800 km, an apoapsis altitude of 68,000 km, and a period of about 6.5 days. This orbit exhibits a 9:2 resonance with the Moon’s synodic orbit.4 For this analysis, the specific orbit chosen for the navigation relay is a Distant Retrograde Orbit (DRO) with an average altitude of 75,000 km and a period of about 13 days (but is not in resonance with the NRHO). The orbits appear in Figure 1, as viewed in the rotating system from the Earth-Moon line, below the plane of the Moon’s orbit.
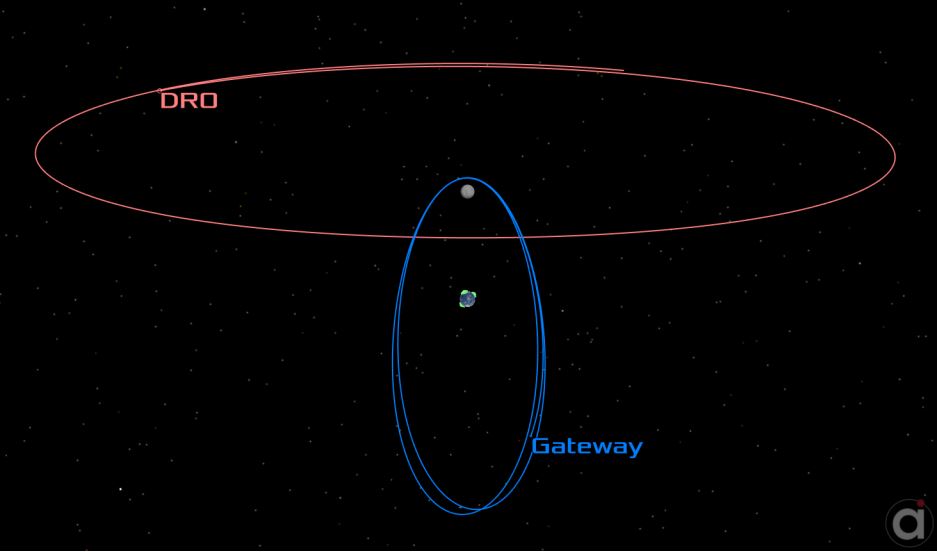
Figure 1: NRHO and DRO Orbit Geometry
The DRO is selected as the relay orbit because it provides at least one distinct advantage for alleviating the burden on the DSN. The stability of the orbit allows for (almost) no OMMs.15, 16 With no OMMs and an autonomous relative navigation strategy, ground based tracking and telemetry can be minimized to vehicle state-of-health information. These telemetry links can be provided by alternatives to the DSN, such as the Universal Space Network (USN).
The 9:2 resonant NRHO-DRO orbit pairing does not preclude line-of-sight blockages by the Moon. However, the resonant nature of the NRHO does help to provide stable, predictable behavior in this regard. Over the course of one year, the pairing goes through three different ”eclipse” seasons of blockages between the two spacecraft. From the geometry, the lunar blockages only occur when the DRO is near its maximum Y-amplitude (in rotating coordinates) and the NRHO is near the opposite ascending/descending node. Due to the elongation of the NRHO, a spacecraft moves quickly through the plane of the DRO. This means that each blockage is relatively short in duration, typically an hour or so. In total, the amount of blockage time is minimal, totaling only about 14 hours per year. See Figure 2 for a plot of the accumulated blockage time over the course of one year. This analysis covers the time period that incorporates the first set of blockages in the March/April time-frame.
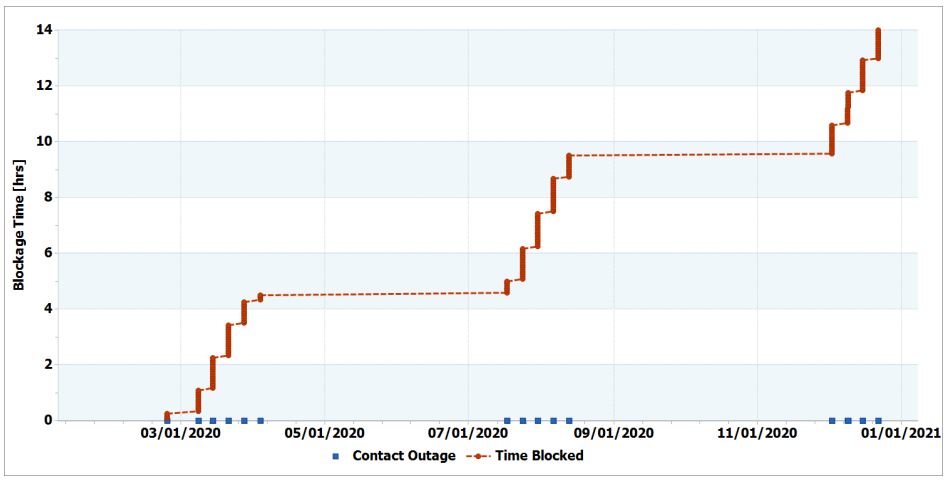
Figure 2: Cumulative NRHO and DRO Contact Outages Over One Year
For Gateway, one method of orbit maintenance under study is a receding-horizon approach for x-axis crossing control.5, 17 Initially, a periodic NRHO in the Circular Restricted Three Body model is used to target a quasi-periodic NRHO in a higher-fidelity ephemeris force model. The resulting quasi-periodic orbits have been extended up to 15 years in duration, and are used as a source of targeting conditions for orbit maintenance maneuvers (OMMs). The receding-horizon approach then targets the reference Rotating Libration Point (RLP) frame x-velocity at periapsis multiple revolutions ahead of the maneuver planning state. These reference trajectories have been generated under both uncrewed and crewed orbital conditions.4
Previous works examining orbit maintenance costs for NRHOs have only used notional (static) navigation errors as part of the maneuver planning process, or have been based on linear covariance analysis.4 To perform a more detailed navigation analysis, a closed-loop simulation is developed that incorporates both realistic navigation errors and maneuver execution errors associated with the receding-horizon orbit maintenance approach. Navigation solutions are computed using simulated tracking data that is processed through a Square-Root Information Filter (SRIF).18, 19 At apoapsis, the receding-horizon approach is used to plan OMMs using the navigation state. Maneuver execution errors are then applied to the truth simulation, while the SRIF is only allowed knowledge of the planned maneuver. This approach allows for navigation errors to realistically affect maneuver planning, and for maneuver execution errors to affect navigation accuracy.
To learn more, you can read our white paper “Examining the Feasibility of Relative-Only Navigation for Crewed Missions to Near Rectilinear Halo Orbits”
Click the image below to download the white paper.
References
1C. Newman, D. Davis, R. Whitley, J. Guinn, and M. Ryne, “Stationkeeping, Orbit Determination, and Attitude Control for Spacecraft in Near Rectilinear Halo Orbits,” AAS/AIAA Astrodynamics Specialists Conference, Snowbird, UT, AAS/AIAA, August 2018.
2K. Hambelton, “Deep Space Gateway to Open Opportunities for Distant Destinations,” Web, 3 2017. NASA.
3R. Whitley and R. Martinez, “Options for Staging Orbits in Cislunar Space,” 2016 IEEE Aerospace Conference, Big Sky, MT, IEEE, March 5-12 2016.
4 D. Davis, S. Bhatt, K. Howell, J. W. Jang, R. Whitley, F. Clark, D. Guzzetti, E. Zimovan, and G. Barton, “Orbit Maintenance and Navigation of Human Spacecraft at Cislunar Near Rectilinear Halo Orbits,” AAS/AIAA Spaceflight Mechanics Meeting, San Antonio, TX, AAS/AIAA, February 5-9 2017. AAS 17-269.
5D. Guzzetti, E. Zimovan, D. Davis, and K. Howell, “Stationkeeping Analysis for Spacecraft in Lunar Near Rectilinear Halo Orbits,” AAS/AIAA Spaceflight Mechanics Meeting, San Antonio, TX, AAS/AIAA, February 5-9 2017. AAS 17-395.
6J. Crusan, “Future Human Exploration Planning: Lunar Orbital Platform – Gateway and Science Workshop Findings,” NASA.gov, March 207 2018. https://www.nasa.gov/sites/default/ files/atoms/files/20180327-crusan-nac-heoc-v8.pdf.
7Wikipedia. Web, June 2018. https://en.wikipedia.org/wiki/Lunar_Orbital_ Platform-Gateway#Proposed_timeline.
8C. Shouraboura, M. D. Johnston, and D. Tran, “Prioritization and Oversubscribed Scheduling for NASA’s Deep Space Network,” Workshop on Scheduling and Planning Applications, International Conference on Automated Planning and Scheduling (SPARK, ICAPS 2016), London, UK, June 2016.
9L. David, “Mars’ Looming Traffic Jam,” Space News Magazine, April 24, 2017.
10NASA, “NASA’s Mission Operations and Communications Services,” October 1, 2014. https://deepspace.jpl.nasa.gov/files/6_NASA_MOCS_2014_10_01_14.pdf.
11K. Hill, G. Born, and M. Lo, “Linked, Autonomous, Interplanetary Satellite Orbit Navigation (LiAISON) in Lunar Halo Orbits,” AIAA/AAS Astrodynamics Specialist Conference, Lake Tahoe, CA, AAS/AIAA, August 7-11 2005. AAS 05-400.
12K. Hill, J. Parker, G. Born, and N. Demandante, “A Lunar L2 Navigation, Communication, and Gravity Mission,” AIAA/AAS Astrodynamics Specialist Conference, Keystone, CO, AAS/AIAA, August 21-24 2006. AIAA 2006-6662.
13P. Liu, X. Hou, J. S. Tang, and L. Liu, “Application of two special oribts in the orbit determination of Lunar satellites,” Research in Astronomy and Astrophysics, Vol. 14, No. 10, 2014, pp. 1307–1328.
14I. Murphy, “Advanced Space Wins $ 250,000 Innovation Award from Colorado Office of Economic Development and International Trade,” Business Wire, June 2017. https://www.businesswire.com/news/home/20180607005363/en/ Advanced-Space-Wins-250000-Innovation-Award-Colorado.
15C. Bezrouk and J. Parker, “Long Duration Stability of Distant Retrograde Orbits,” AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, AAS/AIAA, August 4-7 2014. AIAA 2014-4424.
16G. Turner, “Results of Long-Duration Simulation of Distant Retrograde Orbits,” Aerospace, Vol. 3, No. 4, 2016.
17G. Wawrzyniak and K. Howell, “An Adaptive, Receding-Horizon Guidance Strategy for Solar Sail Trajectories,” AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MN, AAS/AIAA, August 13-16 2012. AIAA 2012-4434.
18G. Born, B. Schutz, and B. Tapley, Statistical Orbit Determination. Elsevier, 1st ed., May 2004.
19C. D’Souza, “On the Square Root Information Filter and Square Root Information Smoother Forumulation,” NASA EG Technical Brief, No. FltDyn-CEV-16-X, 2016.
20C. D’Souza and G. Barton, “Process Noise Assumptions for Orion Cislunar Missions,” NASA MPCV Technical Brief, No. FltDyn-CEV-16-50, August 2016.
21FreeFlyer. Mission Version 7.3.1, 2018. https://ai-solutions.com/freeflyer/.
22R. Zanetti, K. DeMars, and R. Bishop, “Underweighting Nonlin
