Cislunar space has been one of the most up-and-coming topics in our industry. Recent years have brought a lot of activity and attention to the domain.

NASA is leading the way with the Artemis program, which will send infrastructure and humans to the cislunar environment. Artemis 1 successfully completed its mission in 2022, Artemis 2 is scheduled to launch next year, and there are plans for more missions for the next decade and beyond. A crucial aspect of this program is the Gateway, a lunar outpost that allows astronauts to live in deep space for extended periods and prepare for surface missions. The CAPSTONE mission is a testbed for the Gateway’s Near Rectilinear Halo Orbit (NRHO) in cislunar space. Other nations are planning their own human-tended cislunar operations. Outside of the human spaceflight realm, a more commercial endeavor is the NASA Commercial Lunar Payload Services Program (CLPS). This constitutes companies sending scientific equipment and payloads to the moon to deepen our understanding of the lunar surface. Defense operations are also planned for cislunar space, including the United States Space Force Oracle mission.

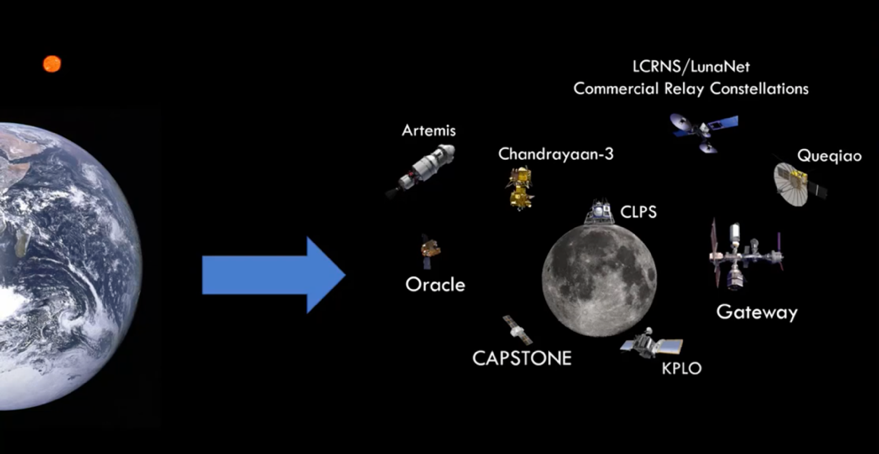
These are just a few instances of recent activity in cislunar space. With this much infrastructure in the domain, there has been a growing need for improved communication, precise positioning navigation, and reliable timing services in lunar missions. Government entities and commercial companies are developing communication relay systems to support this expansion. Effective systems for cislunar trajectory design and operational tools are crucial for the success of these endeavors.

What is Cislunar Space?

Cislunar space is the realm between Earth and the Moon, with the name alluding to the Earth-Moon neighborhood. The region is difficult to define, but its scale is staggering. The distance to the moon is roughly 400,000 kilometers, approximately 100 times the distance from New York to Los Angeles. This is about 300 to 400 times the distance from Earth to Low Earth Orbit (LEO), and about 10 to 11 times the distance to Geosynchronous Earth Orbit (GEO), which is as far as most satellites journey today. Just considering the distance the region is huge, not to mention its volume. Cislunar space, enclosed by the Moon’s orbit, encompasses a volume nearly 10,000 times that of GEO. In terms of defense and surveillance, cislunar space poses both challenges and opportunities. Its sheer vastness demands thoughtful consideration for space operations, especially in a defense context.

Cislunar space is a vast frontier that redefines the scope of space exploration. As we advance into this expansive region, understanding and effectively navigating it are paramount for the future of space exploration beyond Earth. To gain insight into the unique challenges posed by the cislunar environment, we need to explore the fundamental assumptions that shift when transitioning from near-Earth or single-body to multi-body regimes.

Near-Earth Assumption

The Near-Earth assumption posits that Earth’s gravitational pull is the main dominating body in the vicinity of our planet, guiding the trajectories of spacecraft in LEO and GEO. When we venture into the cislunar region of space, this assumption no longer holds true. Unlike near-Earth regions, cislunar space demands a coupled consideration of gravitational fields. Both Earth’s and the Moon’s gravitational forces come into play, and neither can be neglected in most cases. In fact, the coupled nature of the gravitational pull of these two massive bodies becomes a key factor in mission planning such that unique paths can be leveraged.

Earth-Moon Rotating Frame

Near-Earth space calculations rely on an Earth-centered, inertial reference frame. In the cislunar domain, it’s more practical to adopt an Earth-Moon rotating frame. This reference frame anchors Earth and the Moon in a fixed position, allowing analysts to focus solely on the spacecraft’s motion. This shift in perspective streamlines the analysis of spacecraft motion and classifications.

The transition from Near-Earth to cislunar space marks a fundamental shift in our approach. It’s a reminder that as we expand our horizons in space exploration, our assumptions and reference frames must adapt accordingly.

Sensitive Dynamics

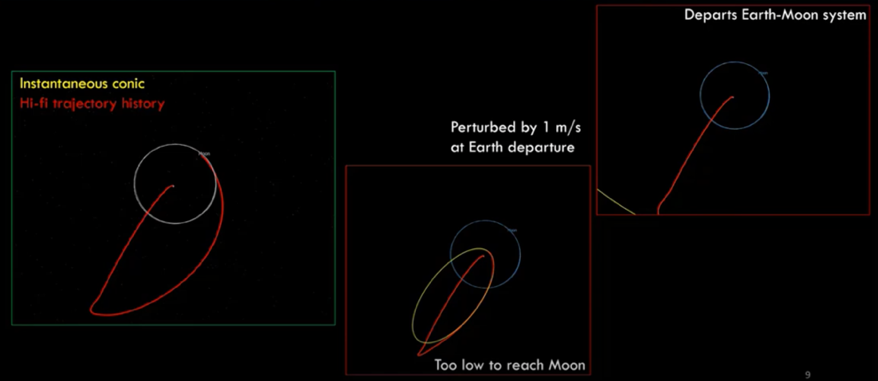
The sensitive, intricate dynamics of the cislunar regime are crucial to be aware of as we expand into the new domain. Imagine a mission departing from Earth to the Moon; this would involve the unique dynamics of cislunar space and leveraging the gravitational forces exerted by the Sun, Earth, and Moon. By synchronizing these dynamics, sensitive trajectories like the instantaneous conic are formed. The sensitivity of these dynamics becomes apparent when considering the impact of minute perturbations. A deviation as small as one meter per second in various directions during launch can yield dramatically different outcomes. It could result in missing the Moon entirely or even escaping the Earth-Moon system altogether. Even the tiniest adjustments can significantly alter the course of a mission. This presents challenges, but also offers unique advantages. Due to sensitivity, spacecraft can navigate cislunar space with relatively low energy expenditures, known as Delta V costs. This characteristic makes cislunar space an intriguing arena for future missions, where a subtle touch can yield efficient travel.

Motion Classification

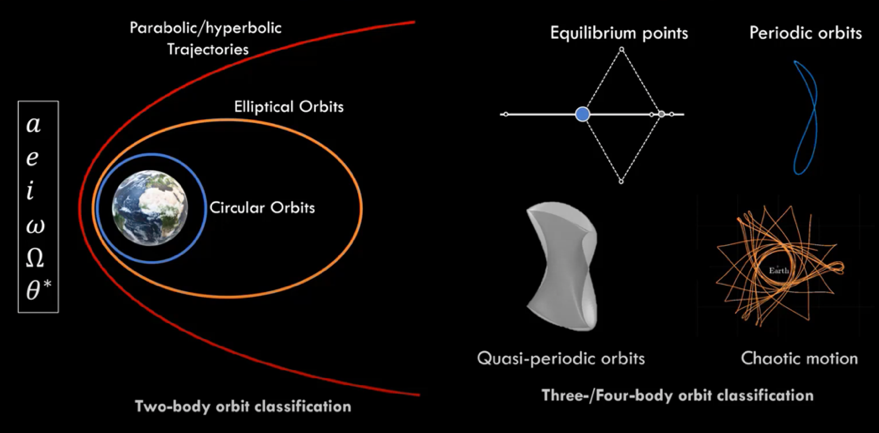
Compared to the Near-Earth realm, classifying motion in cislunar space is far more complex. Traditional two-body classifications, such as conic sections encompassing circular, elliptical, and parabolic/hyperbolic trajectories, prove insufficient in this dynamic environment where Earth and the Moon’s gravitational interplay is present.

Cislunar dynamics introduce equilibrium points, also known as Lagrange points. These are fixed positions within the Earth-Moon system that represent stable regions. Additionally, motion classifications include periodic orbits, quasi-periodic orbits, and chaotic motion, each distinctly shaped by the gravitational influences of both bodies. Uniquely, cislunar space lacks the convenience of orbital elements commonly used for traditional classifications. Cislunar space possesses an entirely new design paradigm that requires new approaches and understanding. Navigating motion in cislunar space is an integral aspect of advancing our capabilities in this realm of space exploration.

Periodic Orbits

The periodic orbits found in cislunar space offer a diverse set of pathways for space missions, differing from the traditional conic orbits. These orbits vary in their geometry, making them advantageous for different mission profiles.

• L₁/L₂Lyapunov Orbit Families: These orbits lie in the Earth-Moon plane, providing practical options for navigation in cislunar space.
• Distant Retrograde Orbit Family: These high-stability orbits exist in the Earth-Moon plane. One served as the destination for the Artemis 1 mission.
• L₁/L₂Halo Orbit Families: These orbits are well-known for their out-of-plane characteristics, making them valuable for accessing specific regions in cislunar space. One of these orbits will serve as the destination for the lunar Gateway.
• L₂ Northern/Southern Butterfly Orbit Families: Each of these orbits are characterized by their unique shape and diverse stability properties. They traverse both the near and far side of the Moon as well as provide high visibility of the lunar poles.
• L₁/L₂Vertical Orbit Families: These orbit families are characterized by their “figure-8” shape, located on the near (L₁) and far (L₂) sides of the Moon.

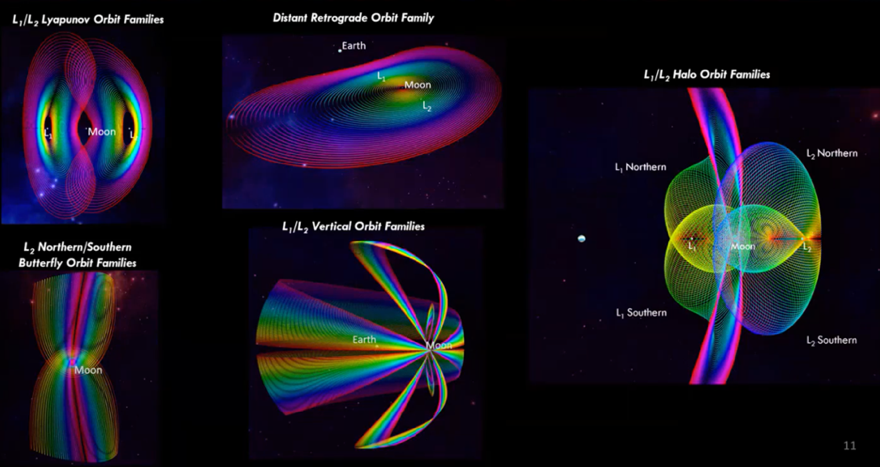
These periodic orbits introduce new possibilities in space exploration, breaking away from traditional conic models to enable missions in previously inaccessible regions.

Quasi-Periodic Orbits

Going beyond periodic orbits, quasi-periodic orbits do not form closed curves, but instead trace paths on a surface. There are various families of quasi-periodic orbits, each offering specific mission advantages.

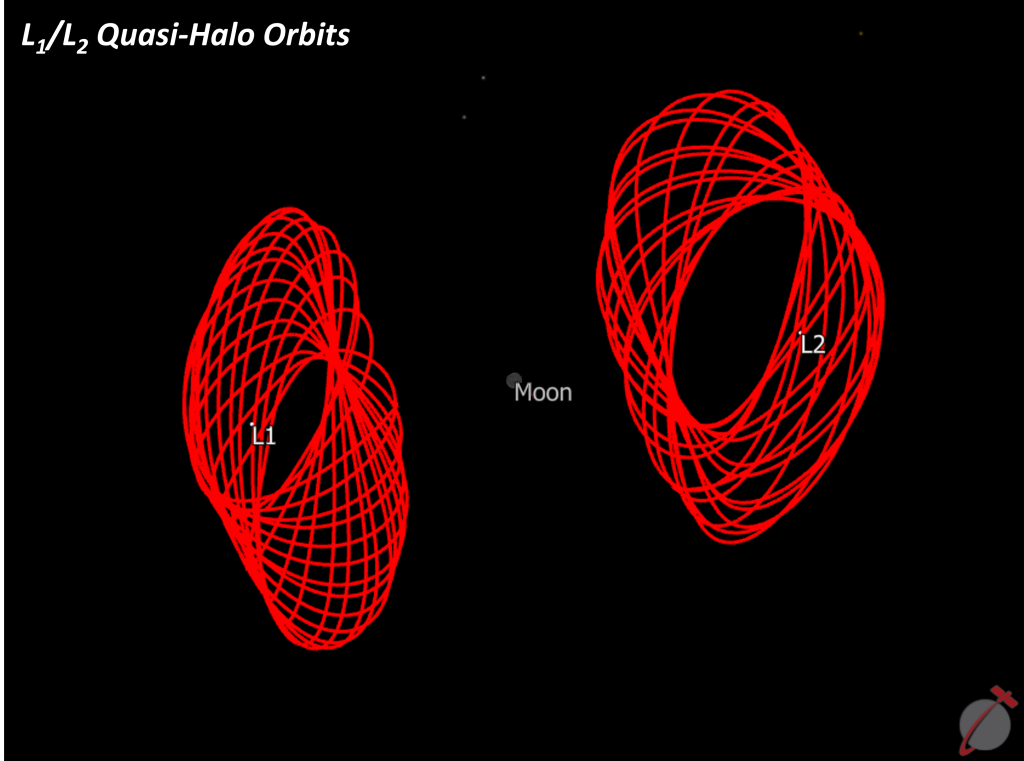
Cislunar space boasts a rich array of possibilities for path planning, catering to a wide range of missions with differing objectives. Periodic and quasi-periodic orbits break free from traditional conic motion, opening new horizons in space exploration in the Earth-Moon neighborhood.

Stable/Unstable Manifolds

In addition to periodic orbits, quasi-periodic orbits, and equilibrium points, there are also stable and unstable manifolds. These provide maneuver-free paths into and out of orbits with minimal energy expenditure, aiding travel for low propellant expenditure. They also serve as fundamental components for crafting cislunar trajectories, adding versatility to space missions.

Models for Cislunar Space

In our quest to understand and model the dynamics of cislunar space, various orbit classifications and models come into play. The Circular Restricted Three-Body Problem (CR3BP) stands out as a widely used and fundamental model, proven particularly effective in preliminary design processes. The CR3BP focuses on the interaction between Earth, Moon, and a spacecraft, assuming that Earth and the Moon are point masses orbiting their common barycenter. The spacecraft is treated as a particle within this system, allowing for relatively simplified modeling. The Hill Restricted Three-Body Problem (HR3BP) and the Elliptic Restricted Three-Body Problem (ER3BP) provide additional models for specific applications.

The inclusion of the Sun into the dynamics introduces Four-Body Models, considering Earth, Moon, Sun, and the spacecraft. Such models are relevant when we need to increase solution fidelity and consider the influence of the Sun on cislunar motion. Some of these include the Bicircular Restricted Four-Body Problem (BCR4BP), Hill Restricted Four-Body Problem (HR4BP), and Quasi-Bicircular Model. These four-body models offer a toolkit for understanding and predicting Sun-perturbed motion in cislunar space, providing the foundation for designing and executing missions within the cislunar realm.

Tools for Trajectory Design

In the realm of cislunar space exploration, the task of trajectory design calls for a set of effective tools. While these tools are not exhaustive, the following stand out for their versatility in different types of analysis.

Multiple Shooting Targeting

Shooting methods are powerful tools in the realm of trajectory design, especially in cislunar space. To illustrate their utility, consider a multiple shooting targeting method traveling from Earth (Point A) to the Moon (Point B). In an ideal scenario there would be initial conditions that fulfill all mission constraints, but this rarely happens. An alternative approach requires breaking the journey into segments or arcs. This could involve simulating three arcs and employing a shooting process to seamlessly connect them. Additional constraints, such as achieving a specific altitude at the Moon, can also be introduced within these shooting problems.

The ultimate goal is to unite all segments into a continuous trajectory that satisfies predefined constraints. It is crucial to ensure that initial guesses closely capture the desired fundamental path such that the desired geometries are preserved. This is vital in cislunar space, where sensitivity to initial conditions necessitates precision in trajectory design and fidelity maintenance.

Other Targeting Methods

Precise cislunar targeting requires a range of methods. Some notable approaches include:

1. Two-Level Targeting: This method breaks up correction of position and velocity of the into separate steps, allowing mission planners to segment the problem into manageable components.
2. Collocation: This technique transforms trajectory design into an implicit Runge-Kutta method, solving the same problem from a different angle.
3. Optimization: This offers gradient-based and non-gradient-based approaches, minimizing cost function and satisfying constraints.

Poincaré Maps

Poincaré maps are unique visual tools that illustrate the repeating behavior of a dynamic system by capturing significant points where trajectories intersect a specific plane or surface. To grasp their significance, think of it as defining a reference plane, either physically or mathematically. On this plane, an initial state is established and projected forward in time. Identifying where the trajectory returns provides valuable insights into cislunar motion.

For example, when a state consistently returns to the same spot on the plane, a periodic orbit is demonstrated. Poincaré maps are especially helpful in extracting order from the chaos of complex data.

Propagating multiple trajectories and recording their periapsis, or closest approach to a planet or Moon, creates a type of Poincaré map, called aPeriapsis Poincaré map, showing intriguing patterns and features. The example below shows concentric ovals that signify highly bounded orbits and a less structured region that suggests more open trajectories. This powerful tool unveils the structure and behavior of cislunar dynamics, facilitating various types of analyses and mission planning.

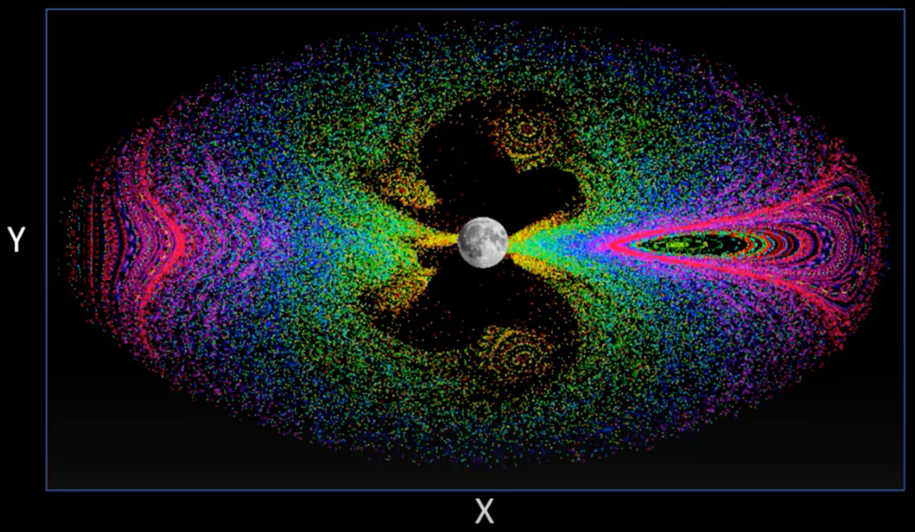
Deep Space Trajectory Explorer

a.i. solutions has been developing the Deep Space Trajectory Explorer (DSTE), a tool that leverages these maps for preliminary design. It has proven particularly valuable for designing missions in the lower fidelity models, primarily focusing on the Circular Restricted Three-Body Problem (CR3BP) and the Four-Body Problem (BCR4BP). Some notable previous applications of the tool include:

• identifying science orbits for ocean worlds of outer planets
• impact and recontact analysis for the lunar Gateway
• higher-dimensional data visualization
• ballistic lunar transfer generation to cislunar libration point orbits
• initial guesses for direct transfers for Artemis

The application of these outlined targeting methods holds promise for the design and execution of successful cislunar missions.

Strategies for Trajectory Design

Considering these tools and the sensitive dynamics of cislunar space, there are three main techniques critical for the trajectory design process in this regime.

Effective Initial Guess Generation Strategies

The trajectory design process relies on targeters and optimizers, all of which necessitate an initial guess without self-starting methods. A robust initial guess strategy is foundational for all differential corrections, optimization, and collocation techniques. It is imperative to remember a good initial guess can yield quick convergence and maintain desired characteristics, while a bad one can result in unpredictable behavior and non-convergence. By leveraging Poincaré maps and isolating desired trajectories, the DSTE has proven effective in initial guess formulation.

Transition of Solutions from Lower to Higher-Fidelity Model

Given the establishment of an initial guess, the solution should then be transitioned from lower-fidelity to higher-fidelity. This is a fundamental practice in engineering design, as starting in a lower-fidelity environment simplifies the complexity of the design process. Low-fi models make certain assumptions about the Earth and Moon’s positions and movements, as well as the spacecraft’s behavior. However, when the time comes for actual operations, the trajectory must align with the high-fi model, which reflects real-world conditions. These transitions should be flexible, accommodating various mission constraints while preserving the characteristics of the initial solutions. A good transition method is flexible for mission constraints and maintains characteristics of initial solutions, while a bad one results in unpredictable behavior and limited ability to maintain desired geometry. The process can reveal discontinuities that are usually addressed with targeting processes to preserve trajectory characteristics. This allows for continuity of mission design and the preservation of operational orbits, even as constraints evolve, and real-world dynamics come into play. At a.i. solutions, we have experience transitioning trajectory solutions from lower-fidelity planning tools such as DSTE high-fidelity flight tools such as FreeFlyer and Copernicus.

Identification of “Families” of Solutions

Instead of relying on isolated point solutions, families of solutions should be identified. This offers a dynamic approach to evolving mission constraints, providing greater flexibility and problem-solving capabilities. Point solutions limit flexibility to inevitable changes in mission constraints. Families of solutions provide greater understanding of flow and expand adaptability in the mission design process.

This concept can occur at various levels of fidelity, spanning from lower to higher. Lower-fidelity models provide a fundamental understanding of the dynamic flow within a specific region of space. Having families of solutions in high-fidelity models serves as a repository of trajectories to address changes in mission constraints. By focusing on solution families, designers can swiftly and effectively respond to changing conditions without having to overhaul the entire trajectory.

It is clear that the paradigm for cislunar trajectory design is unique and distinctive, characterized by sensitive dynamics and the potential for chaotic motion. While these complexities bring a new set of challenges, they also open doors to innovative solutions that can facilitate cost-effective and flexible mission planning. In this context, having the right tools is paramount. At a.i. solutions, we are dedicated to developing advanced flight dynamics tools and capabilities that empower trajectory design by harnessing these unique dynamics, ensuring adaptability, and offering a wide array of options. As we continue to navigate the intricate world of cislunar space, these tools will be instrumental in shaping the future of space exploration and mission success.