Phasing Maneuver

Top Previous Next

In this section, we will discuss phasing maneuvers.

Phasing maneuvers are maneuvers that change the size of the original orbit in order to meet the original orbit at a different point in time. If the spacecraft needs to rendezvous with another spacecraft behind it, it would speed up to increase its period just enough to intercept the other spacecraft. If it needed to catch up to a spacecraft in front of it, the spacecraft would slow down to decrease its period. The maneuver has two burns. The first burn occurs in its original orbit. This shrinks or expands the orbit from its original state. Once the spacecraft completes the orbit and returns to its original burn point, it then performs its second maneuver, matching its original orbit. See the diagram below to see how this works:

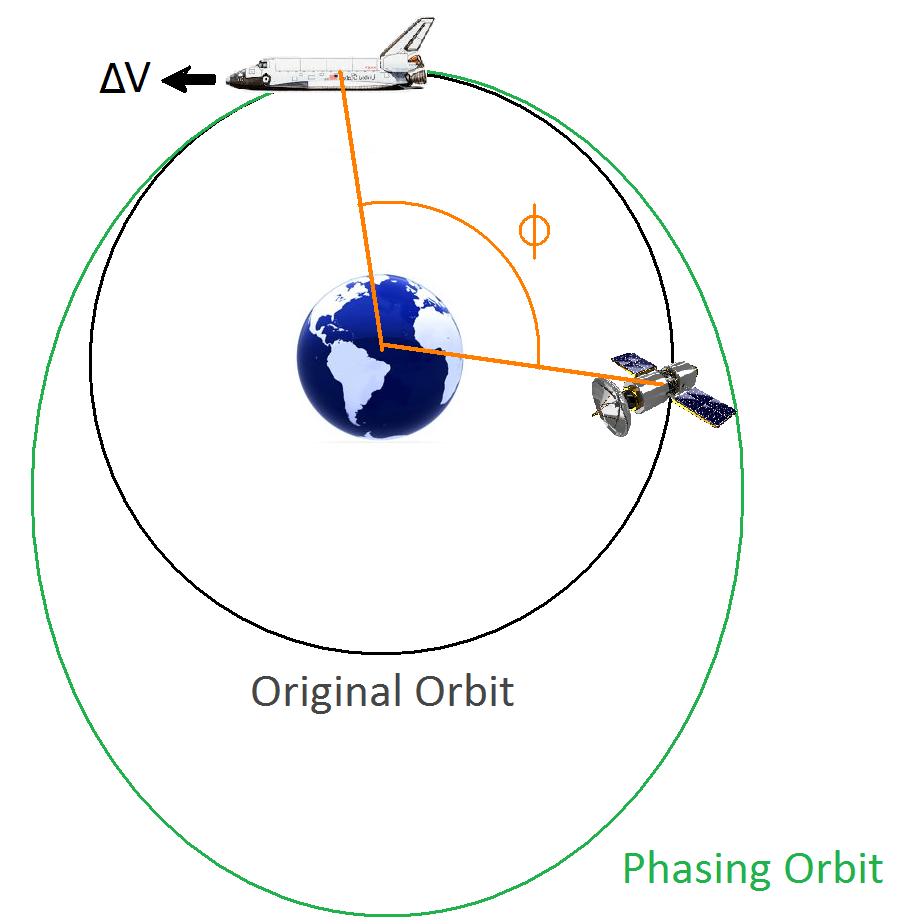
phasingOrbit

Phasing Maneuver Diagram

What can this be used for? In the above diagram, a shuttle uses a phasing maneuver to rendezvous with a satellite that is Φ degrees behind it. Typically when attempting a rendezvous with another spacecraft, phasing maneuvers are used to either slow down or catch up to the target. Also, communications and weather satellites in a geosynchronous orbit that need to move to a different observation area will use a phasing maneuver to move to a different area.

Also, one important thing to note is that sometimes when a spacecraft wants to save fuel, it might make a phasing orbit closer to its original orbit and orbit it multiple times before perfoming its orbital insertion burn. Once it meets up with its target, it will perform its orbital insertion burn.

The rest of this section will cover the following:

1.Calculating Phasing Maneuvers

2.Modeling a Phasing Maneuver

Calculating Phasing Maneuvers

Calculating a phasing maneuver is relatively simple. Think of it as a Hohmann transfer to and from its own orbit. But how do we calculate it by hand?

Problem:

Say we have a geosynchronous satellite with a SMA of 42,164 km, and a true anomaly of 25 degrees. It is currently sitting above the 285 degree longitude line (75° W) observing the DC Metro area. However, this satellite is being re-purposed and needs to be put over the 140 degree longitude line over Japan. How much Δv is required to make a phasing maneuver to move this satellite to its new location? How long will it take to move it there?

Let's take this step by step.

1.Determine how far ahead/behind the target is in time

First, let's see how far behind Japan is in degrees:

θ = 285 - 140 = 145°

Since the Earth has a rotational period of 24 hours, we can calculate the time behind Japan is:

Time behind = (145°/360°) * 24 hr = 34,800 seconds

2.Determine the period needed for the new orbit

Now that we have the time behind, we need to find the period of the new orbit. Since Japan is behind our current position in orbit, we need to slow down to it. This means that we will be expanding our orbit, increasing our SMA, and therefore increasing our period. This means that the new orbit needs to be the "Time Behind" + Our current period.

New Period = Time behind + GEO Period = 34,800s + 86,164s = 120,964 seconds

3.Calculate the SMA of the new orbit

We need to use the following formula to calculate the new SMA:

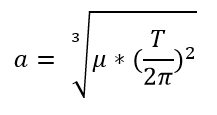Semi-Major Axis as a Function of Orbital Period

With this, we calculate:

a = 52,836.718 km

4.Calculate the Δv needed

The final step of this process is to calculate the current velocity of our spacecraft and the velocity needed to create the correct phasing orbit. To do this, we will use the Vis-Viva Equation.

Current Speed: (rCirc = 42,164 km, aCirc = 42,164 km)

v1 = 3.075 km/s

Phasing Speed: (rPeri = 42,164 km, aPhasing = 52,864.416 km)

v2 = 3.371 km/s

Δv:

Δv = 0.296 km/s

Keep in mind, this Δv value is only for one burn. However, the second burn will be identical to the first in magnitude, but in the opposite direction. If we double this value, we will have the total Δv required for this mission.

Modeling a Phasing Maneuver

Let's use FreeFlyer to test our result.

•Open a new Mission Plan and save it as "GEOPhasing.MissionPlan"

Adding a Spacecraft

•Create a Spacecraft with the following Keplerian elements

oA: 42,164 km

oE: 0

oI: 0 deg

oRAAN: 0 deg

oW: 0 deg

oTA: 25 deg

•In the Spacecraft object's force model, uncheck the "Moon" and "Sun" boxes (this is to make sure no unwanted perturbations occur)

Adding a Spacecraft Sensor

•Click "Sensors" on the left-hand side of the Spacecraft editor

SensorsTab

Sensors Section in the Spacecraft Editor

•Click "Create" to create a Sensor

•Click "Edit Sensor" to open the Sensor editor

sensorCreate

Create and Edit a Sensor

•Change the "Cone Half Angle" to 10 degrees

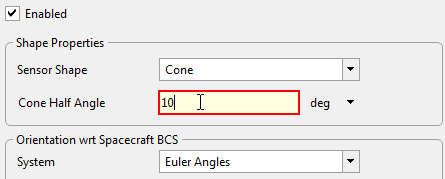
sensorHalfCone

Sensor Cone Half Angle

•Click "Ok" to close the Sensor editor

•Click "Ok" to close the Spacecraft editor

Adding an ImpulsiveBurn

•Create an ImpulsiveBurn object in the Object Browser

•Open the ImpulsiveBurn editor

•Change the attitude system to "VNB"

•Enter the Δv value you calculated earlier into the "Velocity" box of the "Delta-V Directions and Magnitudes" section

•Click "Ok" to close the editor

Adding ViewWindows for Output

•Create a ViewWindow object in the Object Browser

•Open the ViewWindow editor

•Check "Spacecraft1" in the "Available Objects" section

•Check "Show Name" for Spacecraft1

•Change the history mode to "Unlimited"

•Go into "Viewpoints" on the left-hand side

•Change the reference frame to "Inertial"

•Change the declination to 90 deg

•Change the radius to 155,000 km

•Click "Ok" to close the editor

•Clone "ViewWindow1"

•Double-click "ViewWindow1_Copy1"

•Rename it to "ViewWindow2"

•Go into "Viewpoints" on the left-hand side

•Change the type to "2D Map"

•Change the reference frame to "Body Fixed"

•Press "Ok" to close the editor

Building the Mission Sequence

•Drag and drop a "While...End" loop into the Mission Sequence

•Drag and drop a "Step" command inside that While loop

•Drag and drop an "Update" command inside the While loop after the "Step" command

•Drag and drop another "Update" command after the previous one

oModify this "Update" command to update ViewWindow2

•Drag and drop a FreeForm script editor outside of the end of the loop

•Rename the script to "Perform Maneuver 1"

In this FreeForm, we will be changing the color of Spacecraft1, performing the maneuver, then propagating for one full orbit. However, we can't just use "Step Spacecraft1 to (Spacecraft1.OrbitPeriapsis)" since we are already at periapsis. To get around this, we will step the Spacecraft once, and then step to periapsis. To do this we write:

// Changes the spacecraft color for the maneuver

Spacecraft1.Color = ColorTools.Lime;

Maneuver Spacecraft1 using ImpulsiveBurn1;

// Steps the spacecraft, then step it to its periapsis

Step Spacecraft1;

Update ViewWindow1;

Update ViewWindow2;

WhileStepping Spacecraft1 to (Spacecraft1.OrbitPeriapsis);

Update ViewWindow1;

Update ViewWindow2;

End;

Now our Spacecraft will perform the phasing maneuver, and orbit the Earth once.

•In the Mission Sequence, drag and drop another FreeForm script editor at the end of the Mission Sequence

•Rename this FreeForm to "Perform Maneuver 2"

In this script, we will be changing the Spacecraft color and then perform the maneuver. This maneuver is exactly the same in the first maneuver, but in the reverse direction. To adjust this, we can multiply that component by -1. To do this, we write:

// Changes the spacecraft color back to its original color

Spacecraft1.Color = ColorTools.Red;

// Reverses the direction of ImpulsiveBurn1

ImpulsiveBurn1.BurnDirection[0] *= -1;

Maneuver Spacecraft1 using ImpulsiveBurn1;

Next, we need to step the Spacecraft for a day to make sure that we are over our target.

•Drag and drop a "While...End" loop into the Mission Sequence after "FreeForm: Perform Maneuver 2"

•Drag and drop a "Step" command inside that loop

•Drag and drop two "Update" commands after the "Step" command in that loop

oModify the second "Update" command to update ViewWindow2

Your Mission Sequence should look something like this:

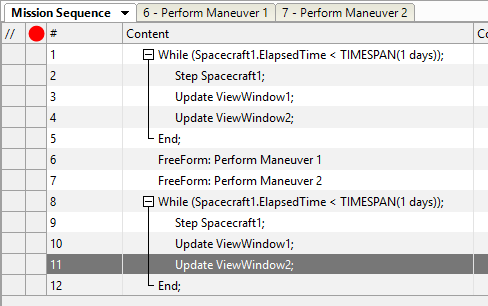
phaseMS

Mission Sequence Example

Save and run your Mission Plan, then try to answer these questions:

Did you end up over your target? Check your sensor view and the line of longitude your Spacecraft is over.

Calculate the Δv values for orbiting a phasing orbit twice. Try putting in those values for the burn. Make sure you adjust the code so the Spacecraft will orbit twice. Was it successful? How much less total Δv was used?