Hohmann transfers are typically the most efficient transfer a spacecraft can make to change the size of an orbit. For simple Hohmann calculations, you must assume circular starting and target orbits - and they must be coplanar!
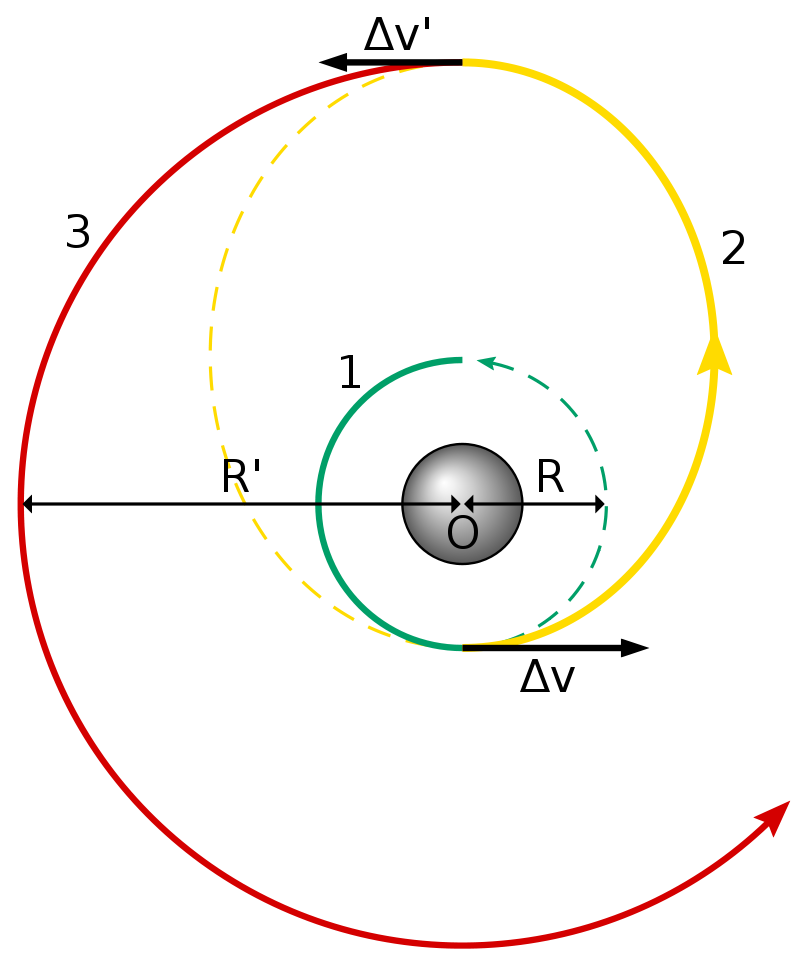
Hohmann Transfer Diagram
In the above diagram, you see a good depiction of a Hohmann transfer. In part 1 (the green orbit), the satellite is in a "parking orbit" which is a Low Earth Orbit that is achieved shortly after launch. In part 2 (the yellow orbit), a maneuver is performed, increasing the velocity of the satellite until its orbit is an ellipse with an apogee at the target orbit's semi-major axis. This part is called the transfer trajectory. Once the spacecraft reaches the apoapsis of that trajectory, it performs an orbital insertion burn. This increases the velocity, matching the orbit to its target circular orbit.
In this section, we will discuss:
1.Calculating Hohmann Transfers
2.Hohmann Transfer - Earth Centered
Calculating Hohmann Transfers
We'll discuss how to calculate the amount of Δv required to perform a Hohmann transfer.
Problem: Our spacecraft has a SMA of 7,000 km and is in a circular orbit. We wish to put it at a 20,000 km SMA circular orbit. Calculate the total amount of Δv required to transfer to the new orbit using a Hohmann transfer. |
Every calculation will be based around the Vis-Viva Equation:
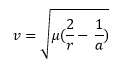
v = Velocity
μ = Standard Gravitational Parameter of the Central Body (398600.442 km3/s2 for Earth)
r = Radius from Earth
a = Orbit Semi-Major Axis
The first step we must take is finding the velocity of the parking orbit. If we use the variables r = 7000 km, a = 7000 km, and the standard gravitational parameter of Earth, we can find v.
vpark = 7.546 km/s
Next, we must find the orbital characteristics of the transfer orbit. First, we must find the semi-major axis of the transfer orbit. To do this, we can take the average of the semi-major axes of the target orbit and the parking orbit.
a = (aTarget + aParking)/2 =(20,000 + 7,000)/2 = 13,500 km
Now, we can find the velocity at periapsis of this transfer orbit. In this case r = 7000 km, and a = 13,500 km. We plug these into the Vis-Viva equation to get:
vtransfer_peri = 9.185 km/s
Then, we can calculate the Δv of the first maneuver:
Δv1 = vtransfer_peri - vpark = 9.185 km/s - 7.546 km/s = 1.639 km/s
This first burn will put our Spacecraft into its transfer orbit. Next, we need to calculate the speed at the transfer orbit's apoapsis. For this calculation, r = 20,000 km, and a = 13,500 km. We plug these into the Vis-Viva equation to get:
vtransfer_apo = 3.215 km/s
Now, we must calculate the velocity of the target orbit. For the variables, r = 20,000 km, and a = 20,000 km. We plug these into the Vis-Viva equation to get:
vtarget = 4.464 km/s
Now, we can calculate the Δv for the insertion burn, and finally the total Δv:
Δv2 = vtarget - vtransfer_apo = 4.464 km/s - 3.215 km/s = 1.249 km/s
ΣΔv = Δv1 + Δv2 = 2.888 km/s
We can also create a Mission Plan to calculate this for us.
Hohmann Transfer - Earth Centered
In this section, we will write a Mission Plan that will not only visualize a Hohmann transfer, but calculate it for us as well.
•Create a new Mission Plan and save it as "HohmannEarthCentered.MissionPlan"
Building the Mission Sequence
•Drag and drop a FreeForm script editor in the Mission Sequence
•Double Click on the FreeForm script editor
•Rename it "User Input"
In this FreeForm script editor, we will have a space that the user can define the parking orbit SMA and the target orbit SMA. To do this, we will write:
// User input for Hohmann Calculation Variable parkingSMA = 7000; Variable targetSMA = 20000; |
Now, we will move on to calculating the Hohmann transfer.
•In the Mission Sequence, drag and drop a second FreeForm script editor after the "User Input" FreeForm
•Double-click the FreeForm script editor
•Rename it "Hohmann Calculations"
In this FreeForm script editor, we will calculate everything needed for the Hohmann transfer using the same steps as the steps taken in Calculating Hohmann Transfers. First, we will calculate the parking orbit velocity, then the transfer semi-major axis, the velocity of the transfer, and the Δv required for that maneuver. To do this, we will write:
// Parking Speed Orbit Variable vPark = sqrt(Earth.Mu * ( (2/parkingSMA) - (1/parkingSMA) ));
// Semi-Major Axis of the transfer trajectory Variable transfSMA = (targetSMA + parkingSMA)/2;
// Velocity at periapsis of the transfer trajectory Variable vTransfPeri = sqrt(Earth.Mu * ( (2/parkingSMA) - (1/transfSMA) ));
// Delta V of the first maneuver Variable dV1 = vTransfPeri - vPark; |
Next, we need to calculate the the transfer trajectory velocity at apoapsis, the target orbit velocity, the magnitude of the second Δv, and the total Δv. To do this, we write:
// Velocity at apoapsis of the transfer trajectory Variable vTransfApog = sqrt(Earth.Mu * ( (2/targetSMA) - (1/transfSMA) ));
// Velocity of the target orbit Variable vTarget = sqrt(Earth.Mu * ( (2/targetSMA) - (1/targetSMA) ));
// Delta V of the second Maneuver Variable dV2 = vTarget - vTransfApog;
// Total Delta V required Variable totalDV = dV1 + dV2; |
All the calculations for the Hohmann transfer have been performed at this point. Now, we need to move onto visualizing the Hohmann transfer.
Adding a Spacecraft
•Create a Spacecraft object through the Object Browser
•Give the Spacecraft the following Keplerian elements:
oA: 7000 km
oE: 0
oI: 0 deg
oRAAN: 0 deg
oW: 0 deg
oTA: 0 deg
So that we can ensure the Spacecraft SMA is the same as the one the user defined, double-click the "Hohmann Calculations" FreeForm script editor and add the following statement to the bottom:
// Assigns the Parking SMA to the spacecraft Spacecraft1.A = parkingSMA; |
Adding the ViewWindow
•Right-click the Object Browser and add a ViewWindow object
•In the ViewWindow editor, make sure that Spacecraft1 is checked under "Available Objects"
•Check "Show Name" for Spacecraft1 as well
•For the history mode, change it to "Unlimited" (this will help us visualize it better)
•Go to "Viewpoints"
•Change the reference frame to "Inertial"
•Press "Ok" to close the ViewWindow editor
Adding ImpulsiveBurns
•Right-click on the Object Browser to create an ImpulsiveBurn
oAdd → Spacecraft Related → ImpulsiveBurn
•Double-click on "ImpulsiveBurn1"
•Change the attitude system to "VNB". This configures the ImpulsiveBurn such that the primary burn direction is in the Velocity direction.
•Right-click "ImpulsiveBurn1" and Clone it
•Rename the cloned object to "ImpulsiveBurn2"
Building the Mission Sequence
•Drag and drop a While loop at the end of the Mission Sequence
•Change the While loop argument to "Spacecraft1.ElapsedTime < TIMESPAN(2 hours)"
•Drag and drop a Step command inside of the While loop
•Drag and drop an Update command inside of the While loop after the Step command
•After the While loop, add a FreeForm script editor
•Open the FreeForm script editor and rename it to "Perform Maneuver 1"
In this FreeForm, we will change the color of the Spacecraft tail, perform the first maneuver, then step to the Spacecraft object's apoapsis. To do this, we write:
// Changes color of SC tail Spacecraft1.Color = ColorTools.Yellow;
// Assigns the calculated delta v value to the Impulsive Burn ImpulsiveBurn1.BurnDirection[0] = dV1;
Maneuver Spacecraft1 using ImpulsiveBurn1;
// Steps the Spacecraft to apoapsis and visualizes the Spacecraft WhileStepping Spacecraft1 to (Spacecraft1.OrbitApoapsis); Update ViewWindow1; End; |
•Drag and drop another FreeForm script editor into the Mission Sequence after "Perform Maneuver 1". Name this "Perform Maneuver 2".
In this FreeForm, we will change the color of the Spacecraft again and perform the second maneuver. Then, we'd like to report the magnitude of each maneuver, and the total Δv of the transfer. To do this, we write:
// Changes the color of SC tail again Spacecraft1.Color = ColorTools.Lime;
// Sets the calculated delta v to the Impulsive Burn ImpulsiveBurn2.BurnDirection[0] = dV2;
Maneuver Spacecraft1 using ImpulsiveBurn2;
// Reports the delta v values Report dV1, dV2, totalDV; |
We are done writing script for this mission. Now let's add in another final While loop to visualize the rest of the mission.
•In the Mission Sequence, drag and drop a While loop at the end of the sequence
•Drag and drop a Step command inside of the While loop
•Drag and drop an Update command inside of the While loop after the Step command
Your Mission Sequence should look something like this:
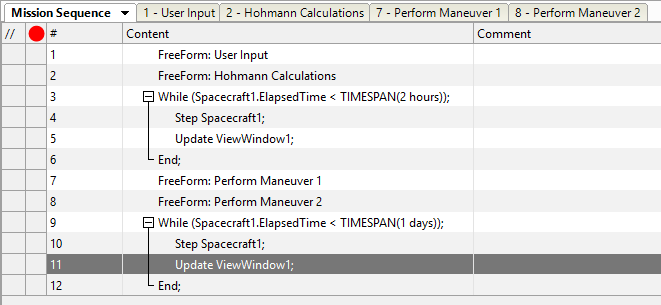
Mission Sequence Example
Save and run your Mission Plan, then try to answer these questions:
Were the delta-v calculations close to the ones we calculated by hand?
Change the parking orbit to a SMA of 9000 km. Run the simulation again. Does the amount of required Δv increase or decrease with larger parking orbits?