Plane change maneuvers are known as one of the more costly maneuvers for spacecraft to perform. However, the math for them is relatively simple. In fact, you only need to have a basic understanding of trigonometry and vector math to calculate the Δv needed in a plane change.
Say we wanted to make an inclination change. If we burned normal to the orbital plane, we would be adding Δv in the y direction of the VNB attitude system. However, this would make our resultant vector larger than what we started with, thus changing the shape of the orbit. See the diagrams below:
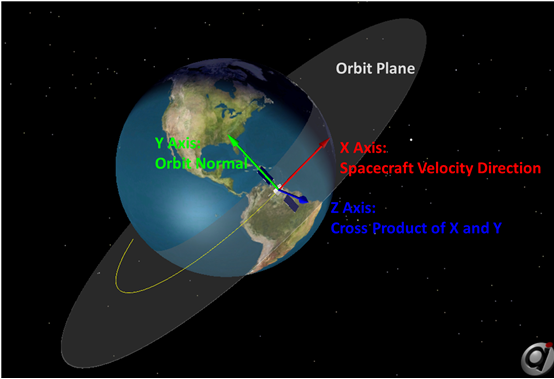
VNB Attitude System
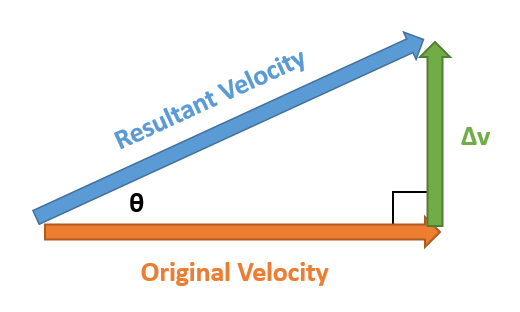
Burn in the Normal Direction
Our resultant velocity is the hypotenuse in this triangle. Because of that, it will definitely be larger than our original velocity. With this, we are not only changing the inclination of the orbit, but we are changing the eccentricity. How can we burn in such a way that the resultant velocity vector has the same magnitude as our original velocity and not change the eccentricity of the orbit? The trick is to tilt the Δv vector backwards. Doing this, we will get an isosceles triangle like the diagram below:
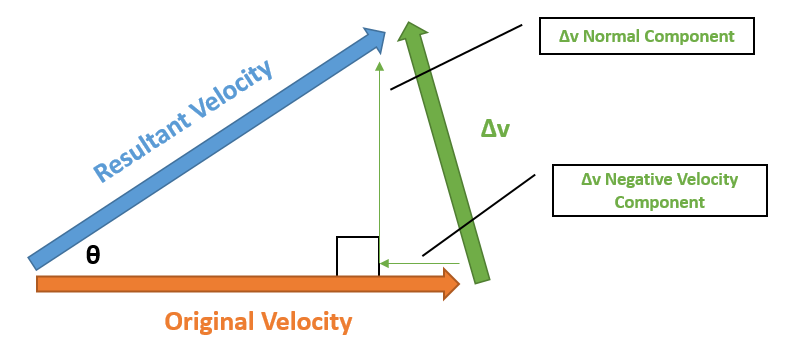
Inclination Change Burn
With this, we can break down the Δv vector into two components: the normal component, and the negative velocity component. Using trigonometry, we can calculate these values quite easily. The formulas for the the Δv are as follows:

Now that we have worked out the math, let's try writing a Mission Plan that calculates and performs a plane change.
Modeling Plane Change Maneuvers
Problem: We have a spacecraft in a circular, equatorial orbit with a SMA of 7200 km. How much Δv would we need to change the inclination to 30º without changing the shape of the orbit? |
We can build our own calculator for this in FreeFlyer. But first, let's add in the necessary objects in the Object Browser.
•Open a new Mission Plan and save it as "CircularPlaneChange.MissionPlan"
Adding a Spacecraft
•Create a new Spacecraft with the following orbital elements:
oA: 7200 km
oE: 0
oI: 0 deg
oRAAN: 0 deg
oW: 0 deg
oTA: 0 deg
•Create a new ImpulsiveBurn object
•Open the ImpulsiveBurn editor
•Change the attitude system to "VNB"
•Click "Ok" to close the editor
Adding the ViewWindow
•Create a new ViewWindow object
•Open the ViewWindow editor
•Check "Spacecraft1" in the "Available Objects" section
•Check "Show Name"
•Change the history mode to "Unlimited"
•Go into "Viewpoints" on the left-hand side
•Change the reference frame to "Inertial"
•Click "Ok" to close the editor
Building the Mission Sequence
•Drag and drop a FreeForm script editor into the Mission Sequence
•Name this "Calculate Plane Change"
In this script, we will assign an inclination angle, calculate the Δv required, and assign it to the ImpulsiveBurn object To do this, we write:
// Inclination to change to in degrees Variable theta = 30; theta = rad(theta);
// Calculate the plane change Variable norm = Spacecraft1.VMag * sin(theta); Variable negVel = Spacecraft1.VMag * ( 1 - cos(theta));
// Assigns the values to the burn ImpulsiveBurn1.BurnDirection = { -negVel, norm, 0}; |
Remember, we are using the VNB attitude system. This is why we need to put a negative sign in front of the "negVel" variable, as VNB's x-component is the positive direction of the velocity vector.
Now, let's propagate the Spacecraft for a day so we can visualize its original orbit.
•In the Mission Sequence, drag and drop a "While...End" loop
•Inside that loop, drag and drop a "Step" command
•Drag and drop an "Update" command after the "Step" command inside the loop
•Drag and drop a FreeForm script editor below the While loop
•Rename this to "Perform Plane Change"
In this FreeForm, we need to change the Spacecraft object's color, maneuver the Spacecraft, and report the total Δv used for the plane change. To do this, we write:
// Change the spacecraft tail color Spacecraft1.Color = ColorTools.Lime;
Maneuver Spacecraft1 using ImpulsiveBurn1;
// Reports the total Delta V used for the plane change Report ImpulsiveBurn1.BurnDirection.Norm(); |
Now, we need to propagate the Spacecraft for one day to visualize the new orbit.
•In the Mission Sequence, drag and drop another "While...End" loop
•Inside the loop, drag and drop a "Step" command
•Drag and drop an "Update" command after the "Step" command inside the loop
Your Mission Sequence should look something like this:
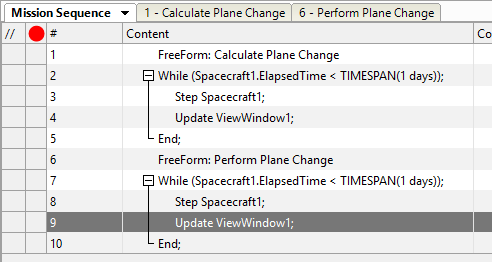
Mission Sequence Example
Save and run your Mission Plan, then try to answer these questions:
Try solving this problem by hand. How do your calculations compare to FreeFlyer's calculations?
Change Spacecraft1's SMA to 30,000 km and run the Mission Plan again. How does the amount of Δv needed change for slower Spacecraft?
If you were to use a bi-elliptic transfer and wanted to perform a plane change as well, where in the transfer would be the most efficient position to perform a plane change?