When we solved the interplanetary Hohmann problem, we found the Δv needed for a spacecraft in an Earth orbit to rendezvous and match a Mars orbit. However, this model is incredibly simplified. In real life, a spacecraft would have to start in a parking orbit around Earth, perform a maneuver, and escape Earth's sphere of influence first. Furthermore, a mission designer would also need to consider the effects of Mars's gravity during the final portion of the problem.
Let's take the problem of finding the necessary Δv to get a spacecraft from Earth to Mars and model it more realistically using the patched conics method. In patched conics, you break down the problem from one multi-body problem to multiple two-body problems. Each body has a "Sphere of Influence" (SOI), or a spherical region around the body where the gravity of that body dominates any spacecraft. When a spacecraft exits that body's SOI, we can then ignore that body's gravity for our calculations, and use a different body instead. So to model an Earth to Mars mission using patched conics, we'd start out calculating things with Earth as the central body. Once the spacecraft exits Earth's SOI, we then ignore Earth and assume the Sun as the central body for the majority of the trajectory. Once we approach Mars and enter Mars's SOI, we then use Mars as the central body. This makes interplanetary missions easier to model and will be more accurate than the Hohmann transfer method as we are considering the gravitational effects of Earth and Mars. The formula for the radius of the Sphere of Influence is as follows:

In this section, we will discuss:
1.Calculating a Patched Conics Problem
2.Modeling a Patched Conics Problem
Calculating a Patched Conics Problem
We can split the patched conics problem into three sections:
1.Elliptical Transfer Orbit
2.Hyperbolic Planetary Departure
3.Hyperbolic Planetary Arrival
Elliptical Transfer Orbit
Say we wanted to calculate a transfer from Earth to Mars using patched conics. The first step is to solve the interplanetary Hohmann transfer problem. The only difference is that this time, we do not need the Δv of the Hohmann transfer (you'll see why soon). What's most important about this part is that we get the phase angle 'Φ', and the closest epoch at which this phase angle occurs. For a reminder on how to determine these, refer to the Interplanetary Hohmann Transfer tutorial.
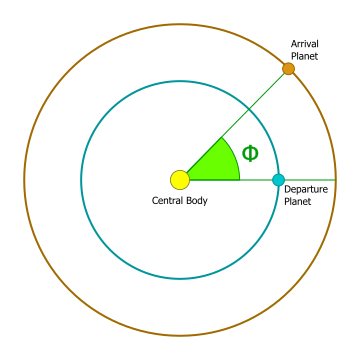
Phase Angle Diagram
Hyperbolic Planetary Departure
The second step is to calculate the necessary maneuver from a parking orbit around Earth to enter into the Hohmann transfer orbit to Mars. To do this, we need a hyperbolic escape trajectory that is parallel to the Earth's velocity vector. In order to escape Earth's gravitational influence, the spacecraft needs to arrive at the sphere of influence with a "hyperbolic excess velocity" v∞ greater than zero.
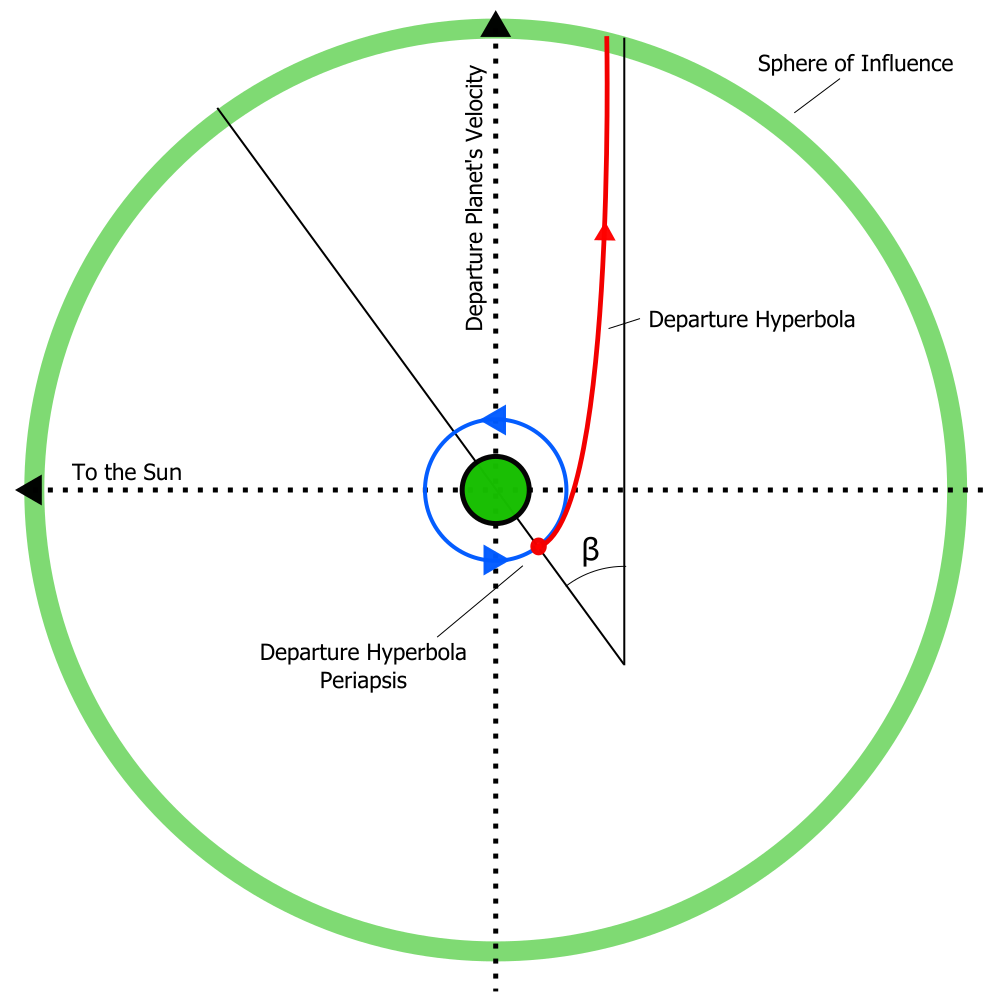
Hyperbolic Escape Trajectory
To enter the Hohmann transfer orbit, v∞ must be the correct amount to place the spacecraft on the desired elliptical trajectory. The required v∞ is equal to the difference between Earth's orbital velocity around the Sun and the velocity the spacecraft needs to have at the periapsis of the transfer orbit:

Since we are modeling Earth's orbit as perfectly circular, we can determine Earth's orbital velocity simply from the circular velocity equation:

We can determine vTransE from the Vis-Viva equation, since the spacecraft's position with respect to the Sun at the periapsis of the transfer orbit is simply equal to Earth's orbit radius:

Plugging these in to our original equation for v∞ and performing a bit of algebra yields:

Now that we have v∞, we need to solve for what the velocity should be at the periapsis of that hyperbolic escape trajectory, vp. But in order to do that, we must first find the 'a' of the hyperbolic orbit. In the Vis-Viva equation, our 'r' will be the radius of the SOI, and our velocity will be v∞ . If we solve for 'a', we will have the following formula:

Now that we have the hyperbolic semi-major axis, we can solve for what our velocity at our periapsis (vp) needs to be. Once again, we can use the Vis-Viva equation.

Then, our Δv is simply the difference between vp and our parking orbit velocity:
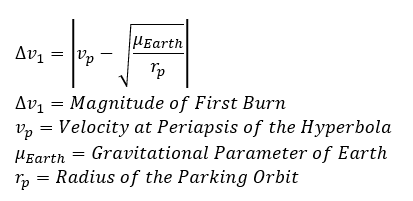
We have now solved for the magnitude of our maneuver to depart Earth! Still, we need to know where to burn. In the hyperbolic escape trajectory diagram, you'll notice there is an angle 'β'. This is the angle between the apse line of the escape hyperbola, and the line parallel to the planet's velocity vector. The formula for this angle is as follows:
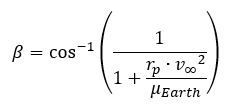
We now have all the necessary information for the Earth centered portion of our patched conics problem. After departing Earth for the Hohmann transfer orbit, we just propagate our Spacecraft as it orbits the Sun until it reaches Mars's SOI. Let's move on to the third, and final portion - the planetary arrival.
Hyperbolic Planetary Arrival
Once we enter the target planet's SOI, we can then assume the central body to be the target planet. Our arrival trajectory should be hyperbolic like the diagram below:
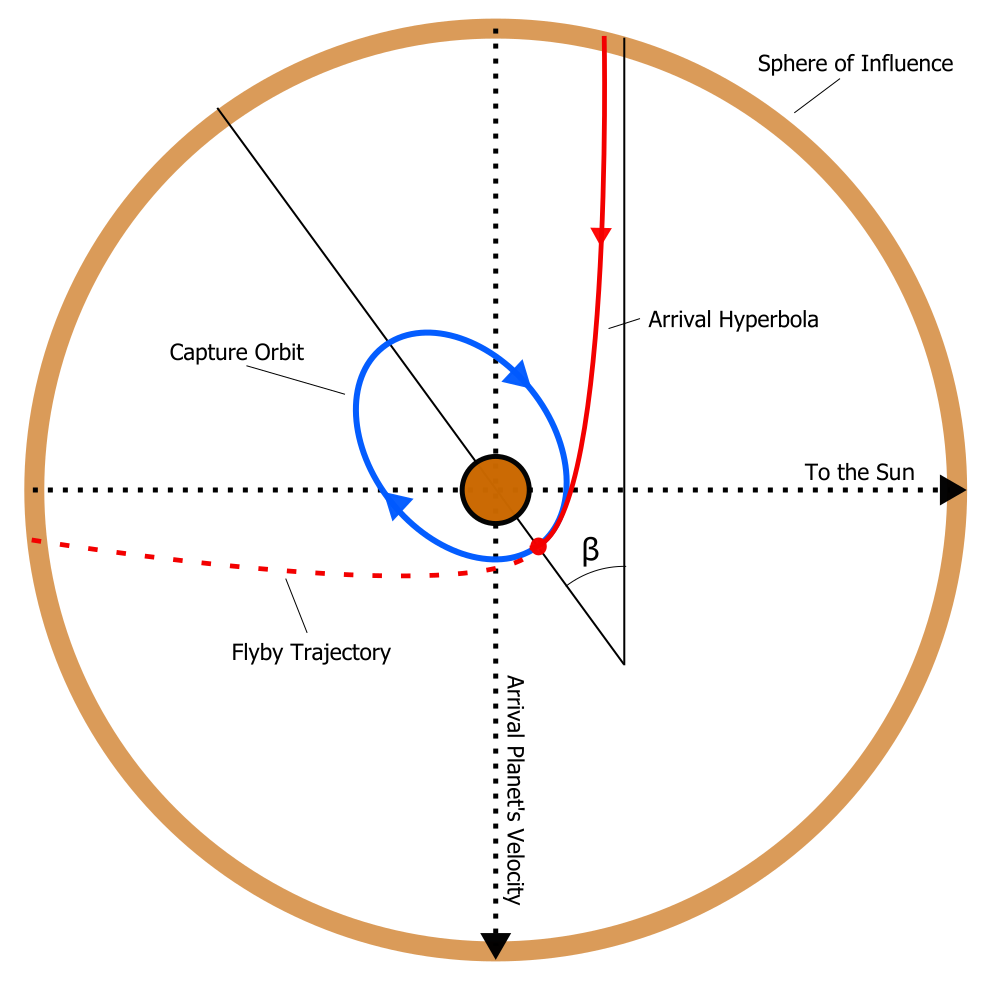
Hyperbolic Arrival Trajectory
If we wish to achieve an orbit around the target planet, it is most efficient to perform an orbital insertion burn at the periapsis of the hyperbolic trajectory. This Δv will be negative as we are slowing the Spacecraft down. How much Δv would we need? Really, it all depends on what you would like your target orbit to be. For our example, we will simply burn into a circular orbit with a radius equal to the periapsis distance of the hyperbolic arrival trajectory. Therefore, the velocity that we need to achieve with our burn is equal to the circular velocity for an orbit around Mars at our given radius, and the magnitude of our second burn is simply the difference between the spacecraft's velocity and the circular velocity:

Note that it is possible to target a specific radius for our final orbit; however, for the purposes of this guide, simply using the periapsis distance upon arrival will suffice. Mission designers could adjust the orbit after the circular insertion with further maneuvers. For more information regarding aiming for a specific periapsis radius, consult "Orbital Mechanics for Engineering Students" by Howard Curtis.
Now we have all of the necessary calculations for a patched conics transfer.
Modeling a Patched Conics Transfer
Problem: Assume that Earth and Mars are in circular orbits around the Sun at 1 AU and 1.524 AU respectively. Model an interplanetary mission from Earth to Mars from a 7000 km SMA parking orbit around Earth all the way to a final orbit around Mars. |
For this tutorial, we will be writing the Mission Plan almost entirely in FreeForm. We also need to create CelestialObjects that will be perfectly circular and coplanar versions of the real planets, as our equations require circular, coplanar orbits. We will refer to these CelestialObjects as "idealEarth" and "idealMars".
•Create a new Mission Plan and save it as "InterplanetaryPatchedConics.MissionPlan"
•Create a Spacecraft through the Object Browser (Don't worry about modifying any of the elements. We will be doing that later)
•Create an ImpulsiveBurn object through the Object Browser
•Double-click on "ImpulsiveBurn1" to open the editor
•Change the attitude system to "VNB"
•Click "Ok" to close the editor
•Right click on "ImpulsiveBurn1" and select "Clone"
•Rename "ImpulsiveBurn1_Copy1" to "ImpulsiveBurn2"
Creating Ideal Planets
•Drag and drop a FreeForm script editor into the Mission Sequence
•Rename this FreeForm script editor to "Create Ideal Planets"
In order to create the ideal planets and set up the ViewWindows through script, you need a more advanced understanding of FreeFlyer. As this knowledge is beyond the scope of this guide, we recommend that you copy and paste the given example code whenever we say "Copy and Paste the following code into the FreeForm script editor."
•Copy and Paste the following code into the FreeForm script editor
// Creates the Ideal Planets CelestialObject idealEarth; CelestialObject idealMars;
// Configures the ideal Earth CelestialObject
idealEarth.CentralBody = "Sun"; idealEarth.Globe.SurfaceLayer.DaytimeImageFilename = Earth.Globe.SurfaceLayer.DaytimeImageFilename; idealEarth.Epoch = Earth.Epoch; idealEarth.Mu = Earth.Mu; idealEarth.Flattening = 0;
// Gets the Earth Cartesian Elements Array RealPos = Earth.GetPositionAtEpoch(Spacecraft1.Epoch); Array RealVel = Earth.GetVelocityAtEpoch(Spacecraft1.Epoch);
// Assigns the Cartesian state and converts them to a Keplerian State Array CarState = {RealPos[0], RealPos[1], RealPos[2], RealVel[0], RealVel[1], RealVel[2]}; Array KepState = ElementConvert(1, 2, CarState, Sun.Mu);
KepState[0] = 149600000; // Reassigns SMA to approx 1 AU KepState[1] = 0; // Reassigns Eccentricity to 0 KepState[2] = 23.5; // Reassigns Inclination to 23.5 deg KepState[3] = 0; // Reassigns RAAN to 0 deg
// Converts the ideal Keplerian state back to Cartesian CarState = ElementConvert(2, 1, KepState, Sun.Mu);
idealEarth.SetState(CarState); idealEarth.Epoch = Spacecraft1.Epoch;
// Configures the ideal Mars CelestialObject
idealMars.CentralBody = "Sun"; idealMars.Globe.SurfaceLayer.DaytimeImageFilename = Mars.Globe.SurfaceLayer.DaytimeImageFilename; idealMars.Epoch = Mars.Epoch; idealMars.Mu = Mars.Mu; idealMars.Flattening = 0;
// Gets the Mars Cartesian Elements RealPos = Mars.GetPositionAtEpoch(Spacecraft1.Epoch); RealVel = Mars.GetVelocityAtEpoch(Spacecraft1.Epoch);
// Assigns the Cartesian State and converts them to a Keplerian State CarState = {RealPos[0], RealPos[1], RealPos[2], RealVel[0], RealVel[1], RealVel[2]}; KepState = ElementConvert(1, 2, CarState, Sun.Mu);
KepState[0] = 227920000; // Reassigns SMA to approx 1.524 AU KepState[1] = 0; // Reassigns Eccentricity to 0 KepState[2] = 23.5; // Reassigns Inclination to 23.5 deg KepState[3] = 0; // Reassigns RAAN to 0 deg
// Converts the ideal Keplerian State back to Cartesian CarState = ElementConvert(2, 1, KepState, Sun.Mu);
idealMars.SetState(CarState); idealMars.Epoch = Spacecraft1.Epoch; |
Configuring the ViewWindow
•Go back to the Mission Sequence
•Drag and drop another FreeForm script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Configure ViewWindow"
•Copy and Paste the following code into the FreeForm script editor:
ViewWindow ViewWindow1({idealEarth, idealMars, Spacecraft1});
// Set up the default view Viewpoint defaultView = ViewWindow1.CurrentViewpoint;
defaultView.ThreeDView.Source = Sun.ObjectId; defaultView.ThreeDView.Target = Sun.ObjectId; defaultView.ThreeDView.TailReference = Sun.ObjectId;
defaultView.ThreeDView.ReferenceFrame = "inertial";
defaultView.ThreeDView.Radius = 600000000; defaultView.ThreeDView.Declination = 90;
ViewWindow1.CurrentViewpoint = defaultView;
// Set History Mode ViewWindow1.SetHistoryMode(idealEarth.ObjectId, 1); ViewWindow1.SetHistoryMode(idealMars.ObjectId, 1);
ViewWindow1.SetShowName(idealEarth.ObjectId, 1); ViewWindow1.SetShowName(idealMars.ObjectId, 1);
ViewWindow1.SetShowName(Spacecraft1.ObjectId, 1); ViewWindow1.SetHistoryMode(Spacecraft1.ObjectId, 0);
ViewWindow1.SetShowBody(Earth.ObjectId, 0); ViewWindow1.SetShowName(Earth.ObjectId, 0); ViewWindow1.SetShowBody(Moon.ObjectId, 0); ViewWindow1.SetShowName(Moon.ObjectId, 0); ViewWindow1.SetShowBody(Mars.ObjectId, 0); ViewWindow1.SetShowName(Mars.ObjectId, 0); |
Setting Up the Spacecraft
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Set Up Spacecraft"
In this FreeForm script editor, we will be editing the Spacecraft elements and ForceModels through FreeForm instead of how we've typically been modifying Spacecraft. We will set the central body, the Keplerian elements, and the force model for our Spacecraft. We can do this by writing the following:
// Set up Spacecraft in Parking orbit around Earth Spacecraft1.CentralBody = idealEarth.DeclaredName;
// Keplerian elements for Spacecraft1 Spacecraft1.A = 7000; Spacecraft1.E = 0; Spacecraft1.I = 23.5; Spacecraft1.RAAN = 0; Spacecraft1.W = 0; Spacecraft1.TA = 0;
// Add ideal planets to Spacecraft Force Model (Spacecraft1.Propagator AsType RK89).ForceModel.AddForce(idealEarth); (Spacecraft1.Propagator AsType RK89).ForceModel.AddForce(idealMars); |
One more thing we need to do is turn off all forces except for our "idealEarth". During our mission, we will be turning on and off various forces depending on which SOI we are in. But for now, we just need the "idealEarth" forces on. We can do this by adjusting the "UseBodyForce" array of the force model. Each element in the array represents a Solar System body. The bodies, in order, are as follows: Mercury, Venus, Earth, The Moon, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto, the Sun, and then any other custom celestial bodies. If the element has a value of 1, the gravity of the corresponding body is turned on. If it is 0, it is turned off. To manipulate this, we will write:
// Turn off all forces except "idealEarth" (Spacecraft1.Propagator AsType RK89).ForceModel.UseBodyForce = {0,0,0,0,0,0,0,0,0,0, /*Sun*/ 0, /*idealEarth*/ 1, /*idealMars*/ 0}; |
Calculating the Phase Angle
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Calculate Phase Angle"
In this script, we need to calculate what the phase angle needs to be, and at which epoch will that occur. First, we need to calculate the period of the Hohmann transfer orbit and the angular velocities of the planets. To do this, we write:
Variable Pi = acos(-1);
// Set up Variables for the problem Variable rEarth = idealEarth.GetPositionAtEpoch(Spacecraft1.Epoch).Norm; Variable rMars = idealMars.GetPositionAtEpoch(Spacecraft1.Epoch).Norm;
// Semi-major axis of transfer orbit Variable aTrans = (rEarth + rMars)/2;
// Period of the Hohmann transfer orbit Variable THoh = 2*Pi*sqrt(aTrans^3/Sun.Mu);
// Angular Velocities of the planets Variable angVelMars = (360/(2*Pi))*sqrt(Sun.Mu/rMars^3); Variable angVelEarth = (360/(2*Pi))*sqrt(Sun.Mu/rEarth^3); |
Now that we have the Hohman transfer orbit period and the angular velocities of the planets, we can calculate the phase angle, and the phase angular velocity. To do this, we write:
// Phase angle and Phase Angular Velocity Variable phaseAngle = 180 - (1/2) * THoh * angVelMars; Variable angVelPhase = angVelEarth - angVelMars; |
Next, we need to calculate what the phase angle between the planets currently is, and the difference between this and the desired phase angle. Calculating this is just like what we did in the Interplanetary Hohmann Transfer tutorial. To do this, we write:
// Calculates the current phase angle Variable curPhaseAngle = idealEarth.GetPositionAtEpoch(Spacecraft1.Epoch).VertexAngle(idealMars.GetPositionAtEpoch(Spacecraft1.Epoch));
// Determine the difference between the current and desired phase angle Variable angleDiff = curPhaseAngle - phaseAngle; If (angleDiff < 0) then; angleDiff = 360 - abs(angleDiff); // Ensures our phasing time will be in the future End; |
Now we need to calculate how long it will be until the next opportunity, and the epoch of the next opportunity. To do this, we write:
// Calculates the epoch where the planets have the proper phase angle Variable timeToPhase = angleDiff/angVelPhase; TimeSpan phaseEpoch = Spacecraft1.Epoch + TimeSpan.FromSeconds(timeToPhase); |
Stepping to Planetary Phasing
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Step to Planetary Phasing"
In this FreeForm script editor, we will propagate the solar system to the "phaseEpoch" we calculated in the previous FreeForm script editor, and change the viewpoint to an Earth-centered view. To do this, we write:
// Set the Propagator Step Size to 1 day Spacecraft1.Propagator.StepSize = TIMESPAN(1 days);
WhileStepping Spacecraft1 to (Spacecraft1.Epoch == phaseEpoch); Update ViewWindow1; End;
// Change Viewpoint to Earth Centered ViewWindow1.CurrentViewpoint.ThreeDView.Source = idealEarth.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.Target = idealEarth.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.TailReference = idealEarth.ObjectId;
ViewWindow1.CurrentViewpoint.ThreeDView.Radius = 200000;
ViewWindow1.SetHistoryMode(Spacecraft1.ObjectId, 1); |
Calculating the Departure Maneuver
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Calculate Departure Maneuver"
In this FreeForm script, we will be calculating v∞ and vp to find the Δv for the escape trajectory. First, we need to calculate the radius of the sphere of influence for each planet. To do this, we write:
// Calculates the Sphere of Influence for the problem Variable EarthSOI = (idealEarth.Mu/Sun.Mu)^(2/5) * rEarth; Variable MarsSOI = (idealMars.Mu/Sun.Mu)^(2/5) * rMars; |
Next, we need to perform the calculations to find v∞, vp, and Δv, using the equations we derived earlier.
// Required hyperbolic excess velocity for Earth departure Variable vInfEarth = sqrt(Sun.Mu/rEarth)*(sqrt(2 - (rEarth/aTrans)) - 1);
// Semi-major axis of Earth departure hyperbola Variable aHyp = ((2/EarthSOI) - (vInfEarth^2/idealEarth.Mu))^(-1);
// Velocity at periapsis of departure hyperbola Variable vPeri = sqrt(idealEarth.Mu * ((2/Spacecraft1.A) - (1/aHyp)));
// Calculates the departure delta-v and assigns it to the first ImpulsiveBurn Variable dv1 = abs(vPeri - sqrt(idealEarth.Mu/Spacecraft1.A)); ImpulsiveBurn1.BurnDirection[0] = dv1; |
Calculating Beta Angle and Maneuver Time
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Calculate Beta Angle and Maneuver Time"
In this script, we will be calculating the 'β' angle so we can figure out when is the appropriate time for our Spacecraft to maneuver. First, let's calculate 'β' using the formula given earlier. To do this, we write:
// Beta Angle Variable beta = deg(acos(1/(1 + ((Spacecraft1.A * vInfEarth^2)/(idealEarth.Mu))))); |
If we look at the diagram in the "Planetary Departure" section from earlier, 'β' is actually the angle away from Earth's negative velocity vector. So when our Spacecraft is (180 - β) degrees away from Earth's positive velocity vector, we need to maneuver the Spacecraft. First, let's calculate the current angle between the Spacecraft's position and the Earth's velocity vector.
One thing we need to remember is that if we're starting in a prograde parking orbit (for this example, we are), we need to maneuver on the dark side of Earth. Another thing to remember is that there are two points in our orbit where we are (180 - β) degrees away from Earth's positive velocity vector. Because of this, we could be at the correct angle but the wrong side of the planet. To check which side we're on, we can check the z component of the cross product vector. If it is negative, we are on the sunny side of Earth and we need to adjust our angle. If it is positive, we are on the dark side of Earth and we don't need to worry about any corrections. To do this, we write:
// Current angle of spacecraft position to the idealEarth Velocity Vector Variable currentAngle = Spacecraft1.Position.VertexAngle(idealEarth.GetVelocityAtEpoch(Spacecraft1.Epoch));
If(Spacecraft1.Position.CrossProduct(idealEarth.GetVelocityAtEpoch(Spacecraft1.Epoch))[2] < 0) then; currentAngle = 360 - currentAngle; End; |
Next, we need to calculate how many degrees we need to travel before performing the maneuver. We do this by subtracting 180 degrees from our current angle and adding β. However, if our calculations concluded that we were on the sunny side of Earth, we need to add 360 degrees to our current angle. To do this, we write:
Variable degreesToTravel = currentAngle - 180 + beta;
If(degreesToTravel < 0) then; degreesToTravel += 360; End; |
Now we need to calculate the angular velocity of the Spacecraft's orbit, and the epoch at which we need to perform the maneuver. To do this, we write:
// Angular Velocity of the spacecraft Variable angVelSC = (360/(2*Pi)) * sqrt(idealEarth.Mu/Spacecraft1.A^3);
// Calculates when the maneuver should be performed Variable timeToManeuver = degreesToTravel / angVelSC; TimeSpan maneuverEpoch = Spacecraft1.Epoch + TimeSpan.FromSeconds(timeToManeuver); |
First Maneuver and Stepping to the SOI
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script editor to "Perform First Maneuver, Step to Earth SOI"
In this script, we need to step to the maneuver epoch (which corresponds to the correct beta angle), maneuver, and then step to the edge of Earth's SOI. First, we need to change the propagator size from 1 day to approximately 600 seconds, then step to the maneuver epoch. We need to make our step size shorter because we are going from observing a heliocentric orbit to observing a Earth centered orbit. To do this, we write:
// Changes the Step Size to 600s Spacecraft1.Propagator.StepSize = TIMESPAN(600 seconds);
WhileStepping Spacecraft1 to (Spacecraft1.Epoch == maneuverEpoch); Update ViewWindow1; End; |
Now that we are at the proper maneuvering time, we need to maneuver the Spacecraft. To visualize this better, we will also change the tail color. To do this, we write:
Spacecraft1.Color = ColorTools.Cyan; Maneuver Spacecraft1 using ImpulsiveBurn1; |
Next, we need to propagate the Spacecraft to the edge of Earth's SOI. Once we do that, we need to change the Spacecraft's central body to the Sun, turn off the gravity of "idealEarth", and turn on the gravity of the Sun. To do this, we write:
// Steps the spacecraft to the edge of the SOI WhileStepping Spacecraft1 to (Spacecraft1.Radius >= EarthSOI); Update ViewWindow1; End;
Spacecraft1.CentralBody = "Sun";
// Turn off all forces except "Sun" (Spacecraft1.Propagator AsType RK89).ForceModel.UseBodyForce = {0,0,0,0,0,0,0,0,0,0, /*Sun*/ 1, /*idealEarth*/ 0, /*idealMars*/ 0}; |
Stepping to the Mars SOI
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Propagate to Mars SOI"
In this FreeForm script editor, we will change the view to be Sun centered, change the step size to 1 day, and then step until we're inside the Mars SOI. To do this, we write:
// Change Viewpoint to Sun Centered ViewWindow1.CurrentViewpoint.ThreeDView.Source = Sun.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.Target = Sun.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.TailReference = Sun.ObjectId;
ViewWindow1.CurrentViewpoint.ThreeDView.Radius = 500000000;
Spacecraft1.Propagator.StepSize = TIMESPAN(1 days);
// Change CentralBody to idealMars to use the Radius property to determine SOI entrance Spacecraft1.CentralBody = idealMars.DeclaredName;
WhileStepping Spacecraft1 to (Spacecraft1.Radius <= MarsSOI); Update ViewWindow1; End; |
At this point, we are inside the SOI of "idealMars." We now need to turn on the gravity of "idealMars." To do this, we write:
// Turn off all forces except "idealMars" (Spacecraft1.Propagator AsType RK89).ForceModel.UseBodyForce = {0,0,0,0,0,0,0,0,0,0, /*Sun*/ 0, /*idealEarth*/ 0, /*idealMars*/ 1}; |
Performing the Intercept Maneuver
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Calculate and Perform Intercept Maneuver"
In this FreeForm script editor, we will be changing the viewpoint, changing the step size, propagating to the hyperbolic periapsis, and then performing an orbital insertion burn. First, let's change the step size, viewpoint, and propagate to the orbit periapsis. To do this, we write:
// Change the step size to 6 hours Spacecraft1.Propagator.StepSize = TIMESPAN(6 hours);
// Change the viewpoint to Mars centered ViewWindow1.CurrentViewpoint.ThreeDView.Source = idealMars.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.Target= idealMars.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.TailReference = idealMars.ObjectId; ViewWindow1.CurrentViewpoint.ThreeDView.Radius = 1500000;
WhileStepping Spacecraft1 to (Spacecraft1.OrbitPeriapsis); Update ViewWindow1; End; |
Now that we are at the periapsis of the approach hyperbola, we need to perform the orbital insertion burn to enter our desired circular orbit. We will use the formula determined earlier for the second burn to calculate our Δv. To do this, we write:
// Required burn to enter a circular orbit Variable dv2 = abs(Spacecraft1.VMag - sqrt(idealMars.Mu/Spacecraft1.Radius));
ImpulsiveBurn2.BurnDirection[0] = -dv2; |
Notice that we are using the VMag property here to access the Spacecraft's velocity at periapsis. Also notice that we assign the burn value to be negative Δv, since we need to slow down (burn opposite to the current velocity direction) to achieve our circular orbit.
Now that we have our maneuver set up, the next step is to perform the maneuver, and then propagate for 100 days to see if we've achieved an orbit. Also, let's report the amount of Δv needed for this mission. To do this, we write:
// Perform the orbital insertion burn Spacecraft1.Color = ColorTools.Lime; Maneuver Spacecraft1 using ImpulsiveBurn2;
WhileStepping Spacecraft1 to (Spacecraft1.ElapsedTime == TIMESPAN(100 days)); Update ViewWindow1; End;
// Report Delta V Values Report dv1, dv2, (dv1 + dv2); |
Your Mission Sequence should look something like this:
Mission Sequence Example
Our mission is now complete!
NOTE: It is important that you do not manually change the view during the mission. This will override the automatic view changing written in our script.
Save and run your Mission Plan, and try to answer these questions:
How much Δv was required for the first manuver? The second?
How much Δv was used total?
What was the periapsis distance (from the Spacecraft to the center of Mars) of the arrival hyperbolic trajectory?
See Also
•Previous Topic: Interplanetary Hohmann Transfer