In the Patched Conics Transfer tutorial, we had a spacecraft enter Mars's SOI and perform an orbital insertion burn. But what would happen if we let the spacecraft continue on it's hyperbolic trajectory? Doing this is called a "Gravity Assist" or "Planetary Flyby."
During a gravity assist, a spacecraft will fly right near another celestial body (typically a planet) and have their flight path be redirected. Also, the spacecraft will leave the SOI with a different velocity than what it entered with. But where does this "extra energy" come from?
When a spacecraft gets really close to a planet during a hyperbolic trajectory, the planet pulls the spacecraft along and swings it around either speeding it up or slowing it down. When the spacecraft enters the SOI the velocity becomes the spacecraft's velocity vector in reference to the Sun subtracted by the planet's velocity vector. After the spacecraft's flyby, once it exits the SOI, you then add the planet's velocity vector to it's velocity in reference to the planet to get the velocity in reference to the Sun. Because the spacecraft exits the SOI in a different direction, there is a change in the magnitude of velocity.
As it turns out, this "free velocity" isn't so free. According to the conservation of energy, the kinetic energy gained by the spacecraft had to be lost somewhere. In actuality, this gravity assist is a conservation of momentum problem. Momentum gets transferred from the planet to the spacecraft. Because the planet's mass is far larger than the spacecraft, the change in velocity is extremely large for the spacecraft, but miniscule for the planet. So, every time a planet is used for a gravity assist, a minute amount of planetary velocity is lost.
In this section, we will discuss:
1.Calculating a Gravity Assist
Calculating a Gravity Assist
Calculating a gravity assist involves understanding hyperbolic orbits and vector math.
The entering heliocentric velocity vector is actually the sum of the entering hyperbolic excess velocity vector and the planet's velocity vector.

The exiting heliocentric velocity vector is the sum of the exiting hyperbolic excess velocity vector and the planet's velocity vector.
![]()
The Δv from the gravity assist is simply this:
![]()
If we substitute the definitions for V2 and V1, then we get the following:
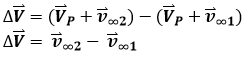
The total Δv from a gravity assist is the difference between the exiting hyperbolic excess velocity vector, and the entering hyperbolic excess velocity vector. You may ask: "If a hyperbola has the same speeds at the entering and exiting points of the SOI, how is there any Δv at all?" Yes, it is true that these two vectors have the same magnitude, but not the same direction. So, the Δv gained from a gravity assist really depends on the change of direction. If we enter and exit the SOI travelling the same direction, there really isn't any Δv gained. However, if we fly closer to the planet, the gravity will bend our path more significantly, increasing our Δv.
Modeling a Gravity Assist
Let's attempt to model a gravity assist in FreeFlyer.
Problem: Two similar spacecraft enter Mars's sphere of influence with the same velocity. One will pass in front of Mars, while the other passes behind Mars. Which spacecraft will end up having the larger orbit around the sun? |
|
FrontSideSC |
BackSideSC |
Central Body |
Mars |
Mars |
a |
-6088.425 km |
-6088.425km |
e |
2 |
2 |
i |
180 |
0 |
Ω |
0 |
0 |
ω |
195 |
45 |
TA |
240.976 |
240.976 |
Tail Color |
Red |
Green |
•Create a new Mission Plan and save it as "GravityAssist.MissionPlan"
Adding in Spacecraft
•Add two Spacecraft through the object browser
•Rename them to the names at the top of the table
•Configure each spacecraft to the elements in the table provided below the problem statement
•In each Spacecraft's force model, check the "Mars" box, and uncheck the "Earth" and "Moon" boxes
•Create a "Vector" object in the Object Browser (we will use this to visualize the direction of the planet's velocity vector)
oRight-click the Object Browser
oAdd → Variables → Vector
Adding the ViewWindow
•Create a ViewWindow through the Object Browser
•Double-click "ViewWindow1" to open the editor
•Check "FrontSideSC", "BackSideSC", and "Vector1" (you will need to expand the list of "Vector" objects in the "Available Objects" to check "Vector1")
•Check "Show Name" for "FrontSideSC" and "BackSideSC"
•Change the History Mode to "Unlimited" for "FrontSideSC" and "BackSideSC"
•Expand the CelestialObject group and select "Mars"
•Check "Show History" for "Mars", and change the History Mode to "Unlimited"
•Go into "Viewpoints" on the left-hand side of the editor
•Change the reference frame to "Inertial"
•Change the source, target, and tail reference to "Mars"
•Change the radius to 300,000 km
•Click on the "Create" button to create a new viewpoint
•Change the name of this new viewpoint to "SolarView"
•Change the title of this viewpoint to "Solar View"
•Change the reference frame to "Inertial"
•Change the source, target, and tail reference to "Sun"
•Change the radius to 500,000,000 km
•Click "Ok" to close the editor
Building the Mission Sequence
•Drag and drop a FreeForm script editor onto the Mission Sequence
•Rename the script to "Set Up Vector"
Whenever you create a Vector object, you must configure it through a FreeForm script editor. In this script, we will set the vector epoch, tell it to draw itself as an arrow, build the vector, and make it visible. To do this, we write:
// Sets up the vector to display Mars's velocity vector Vector1.Epoch = FrontSideSC.Epoch; Vector1.DrawMethod = 1; Vector1.BuildVector(7, Mars); Vector1.Active = 1; |
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Record Initial Data"
In this script, we will save the heliocentric velocity and the hyperbolic excess velocity vectors. To save the the heliocentric vector, we must temporarily reassign both Spacecraft's central bodies to the Sun. Then we can save the vector to an array. To do this, we write:
// Changes the central body to Sun to get the heliocentric velocity FrontSideSC.CentralBody = "Sun"; BackSideSC.CentralBody = "Sun";
Array frontV1 = FrontSideSC.Velocity; Array backV1 = BackSideSC.Velocity; |
Next, we need to reassign the central body to Mars for both Spacecraft. Then we can record the hyperbolic excess speed at entrance to the SOI. To do this, we write:
// Changes the central body back to Mars to get the excess hyperbolic speed FrontSideSC.CentralBody = "Mars"; BackSideSC.CentralBody = "Mars";
Array frontVInf1 = FrontSideSC.Velocity; Array backVInf1 = BackSideSC.Velocity; |
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Propagate Through SOI"
In this script, we will step both Spacecraft until they fly past Mars and reach the edge of the sphere of influence., and record the new velocity data. First, let's calculate the SOI and step to the edge of it. To do this, we write:
// Sphere of Influence of Mars Variable MarsSOI = (Mars.Mu/Sun.Mu)^(2/5) * Mars.GetPositionAtEpoch(FrontSideSC.Epoch).Norm;
While(FrontSideSC.Radius < MarsSOI); Step FrontSideSC; Step BackSideSC to (BackSideSC.Epoch == FrontSideSC.Epoch);
Update ViewWindow1; End; |
Next, we need to record the velocity data so we can calculate the Δv values for each Spacecraft. Also, we can measure the change in direction of each Spacecraft's heliocentric velocity vector. When we record this data, we can record the hyperbolic excess speed, change the central body to the Sun, and then record the heliocentric velocity vectors. To do this, we write:
// Records the data Array frontVInf2 = FrontSideSC.Velocity; Array backVInf2 = BackSideSC.Velocity;
FrontSideSC.CentralBody = "Sun"; BackSideSC.CentralBody = "Sun";
Array frontV2 = FrontSideSC.Velocity; Array backV2 = BackSideSC.Velocity; |
The final thing we need to do in this script is calculating and reporting the numbers.
If we want to find the magnitude of the Δv, we need to subtract the hyperbolic excess speed of the Spacecraft at entrance from the hyperbolic excess speed at exit. One important thing to note is that we need the vector difference between the two before we take the norm. If we subtracted the norm of both velocities, we would get a calculation of '0'.
For the change in direction, we need to take the vertex angles of the heliocentric velocities at entrance and exit of the SOI. If we took the vertex angle between the hyperbolic excess velocity vectors, our change in direction would not be accurate.
One last thing we need to do after reporting the calculations - we need to pause the scenario so that the user can change their 3D view to the "Solar View" that we created earlier. To do this, we write:
// Calculations Variable dVFront = (frontVInf2 - frontVInf1).Norm; Variable dVBack = (backVInf2 - backVInf1).Norm;
Variable dThetaFront = frontV2.VertexAngle(frontV1); Variable dThetaBack = backV2.VertexAngle(backV1);
Report dVFront, dThetaFront, dVBack, dThetaBack;
Pause; |
•Go back to the Mission Sequence
•Drag and drop another Freeform script editor at the bottom of the Mission Sequence
•Rename this FreeForm script to "Propagate Solar System"
In this last script, we are going to change the propagator step size to 1 day (86,400 s), then step the solar system for 1000 days to visualize the new orbits. To do this, we write:
// Change the step size to 1 day FrontSideSC.Propagator.StepSize = TIMESPAN(1 days); BackSideSC.Propagator.StepSize = TIMESPAN(1 days);
While (FrontSideSC.ElapsedTime < TIMESPAN(1000 days)); Step FrontSideSC; Step BackSideSC to (BackSideSC.Epoch == FrontSideSC.Epoch);
Update ViewWindow1; End; |
Your Mission Sequence should look something like this:
Mission Sequence Example
Save and run your Mission Plan. Once the window reports your values, make sure to change your 3D View to the "Solar View". You can do this by selecting the "MissionView" window, and changing the "View Point" dropdown to "Solar View". Once you do that, you can click play on the navigation bar.
Once you've done that, try and answer these questions:
Which Spacecraft had the bigger heliocentric orbit?
In what direction in reference to Mars's velocity vector did that Spacecraft exit the SOI?
How does the magnitude of each Spacecraft's Δv compare? Why are their orbits so drastically different?