Orbit Shapes and Sizes

Top Previous Next

In this section, we will discuss the various aspects of an orbit that make up its shape and size. Two of the six Keplerian elements will be discussed. They are:

1. Semi-Major Axis ('a')

2. Eccentricity ('e')

Semi-Major Axis

The Semi-Major Axis (referred to as 'SMA' or 'a') is the distance from the center of an ellipse to the longer end of the ellipse. In a circle, the SMA is simply the radius.

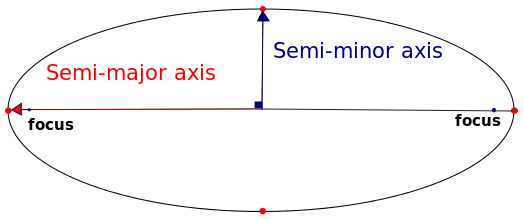
smaDiagram

Semi-Major Axis Diagram

The semi-major axis determines various properties of the orbit such as orbital energy and orbital period. As the semi-major axis increases, so does the orbital energy and the orbital period.

Problem:

We have three spacecraft orbiting at three different semi-major axes. All three spacecraft orbit in a circular, equatorial orbit. Simulate these spacecraft using FreeFlyer and output each Spacecraft object's orbital period.

•Spacecraft 1 - 7,000 km

•Spacecraft 2 - 15,000 km

•Spacecraft 3 - 42,164 km

Let's begin our scenario. Open up a new Mission Plan and label it "SMAPeriod.MissionPlan".

Adding in Spacecraft

•Create a new Spacecraft object by right-clicking the Object Browser on the left-hand side of the Control Screen

•Double-click "Spacecraft1" to open the Spacecraft editor

•Change the element type to "Keplerian"

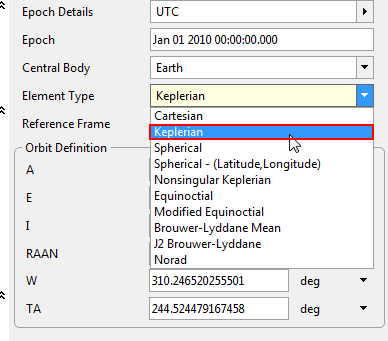
keplerianDropDown

Element Type Dropdown in the Spacecraft Editor

•Put in the following orbital parameters:

oA: 7000 km

oE: 0

oI : 0 deg

oRAAN: 0 deg

oW: 0 deg

oTA: 0 deg

•Click "Ok" to close the Spacecraft editor

•Right-click "Spacecraft1"

•Click "Clone"

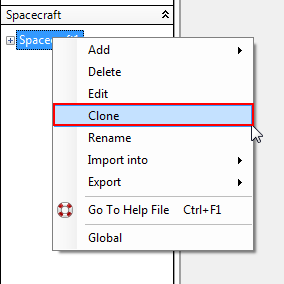
clone

Cloning a Spacecraft

•Double-click "Spacecraft1_Copy1"

•In the top right, rename the Spacecraft to "Spacecraft2"

Note: You can also quickly change a Spacecraft's name by clicking on it in the Object Browser and pressing "F2"

•Change A to 15000 km

•On the left-hand side, click on "Visualization"

•Change the tail color to green

•Click "Ok" to close the Spacecraft editor

•Right-click "Spacecraft2"

•Click "Clone"

•Double-click "Spacecraft2_Copy1"

•Rename the Spacecraft to "Spacecraft3"

•Change A to 42164 km

•Change the tail color to yellow

Adding a ViewWindow

•Create a new ViewWindow by right-clicking the Object Browser

•Double-click "ViewWindow1" to open the ViewWindow editor

•Check each Spacecraft in the "Available Objects" section

•Click on "Spacecraft" to select the group of all three Spacecraft, and check "Show Name"

•Change the "History Mode" to "Unlimited" (all three Spacecraft should still be selected, so this will change the History Mode for all Spacecraft)

•On the left-hand side, navigate to "Viewpoints"

•Click on the "Default" viewpoint

•Change the reference frame to "Inertial"

•Click "Ok" to close the ViewWindow editor

Building the Mission Sequence

•From the Script Elements browser, drag and drop a "While...End" loop into the Mission Sequence

•Change the while loop stopping condition to "Spacecraft1.ElapsedTime < TIMESPAN(2 days)"

•Drag and drop two "Step" commands into the while loop

•The first Step command should say "Step Spacecraft1"

•Double-click the second Step command

•Change the "What to Step" to "Spacecraft2"

•Check the "Step to Condition?" box to step to a condition

•Change the first drop down to "Spacecraft2.Epoch"

•Change the middle dropdown menu from "<" to "=="

•Click on the dropdown that says "0"

•Change "Number" to "Object/Property Method"

•Change the last dropdown to "Epoch"

•The statement should now say "Spacecraft2.Epoch == Spacecraft1.Epoch"

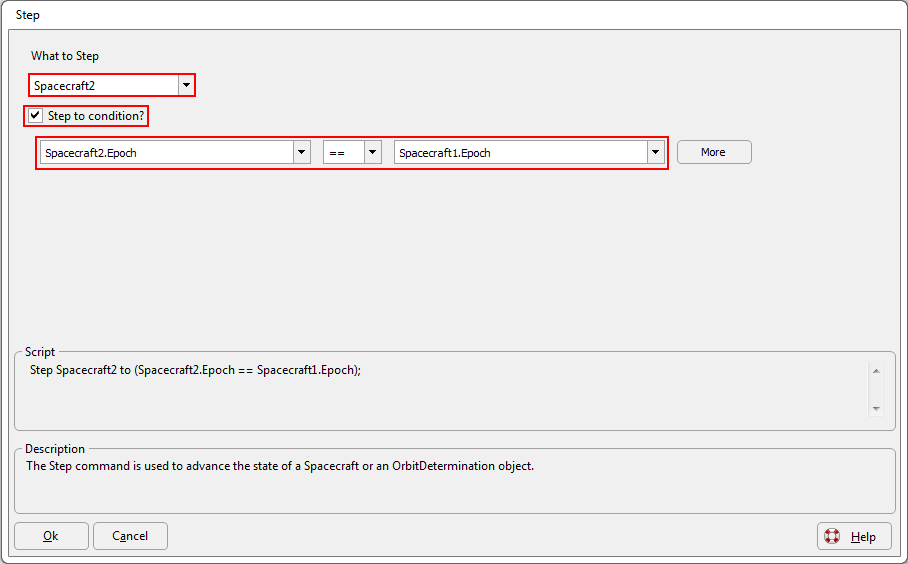
stepBox

Step Command Editor

•Click "Ok" to close the editor

•Clone this command by right-clicking the "Step Spacecraft2" command and click "Clone Selected"

•Change the parameters of the new Step command to say "Step Spacecraft3 to Spacecraft3.Epoch == Spacecraft1.Epoch"

•Drag and drop an Update command into the while loop after the Step commands

Now that we have set up the "Step" and "Update" commands, let's add a FreeForm script editor to report each Spacecraft object's orbital period.

•From the Script Elements browser, drag and drop a FreeForm script editor into the while loop after the "Update" command

•Double-click the FreeForm script editor to open it

•Rename it to "Report Orbital Periods"

This script will be a simple one. It should read as follows:

Report Spacecraft1.Period, Spacecraft2.Period, Spacecraft3.Period;

Now our Mission Plan is ready to run! Your Mission Sequence should look something like this:

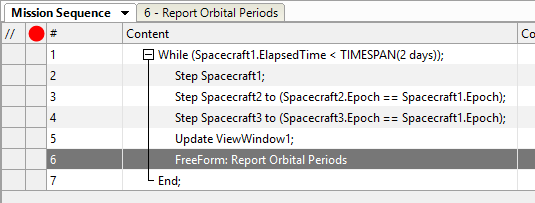
aTutorialMS

Mission Sequence Example

Save your progress and then run to execute the Mission Plan. Then, try to answer these questions:

Which Spacecraft has the shortest period?

Which Spacecraft has the longest period?

What is the significance of Spacecraft3's period?

Eccentricity

Orbital eccentricity is defined as a ratio of the distance between foci to the entire length of the major axis (2x the semi-major axis). Different values of eccentricities determine what kind of orbit exists.

Remember, the eccentricity of an orbit does not affect a Spacecraft object's orbital period or orbital energy. It simply defines the shape of the orbit.

Problem:

We have three spacecraft with the same SMA, but different eccentricities. Use FreeFlyer to plot the Orbital Velocities of these spacecraft and compare them.

For this problem, let's edit the "SMAPeriod.MissionPlan" file that we just made and save it under a different name.

•Open the "SMAPeriod.MissionPlan" file

•Click the "Save As" button (or press CTRL + Shift + S)

•Save the Mission Plan as "Eccentricity.MissionPlan"

We are going to edit each Spacecraft object's Keplerian elements. Edit the semi-major axis and eccentricity to the following:

•Spacecraft1 - A: 30,000 km; E: 0.05;

•Spacecraft2 - A: 30,000 km; E: 0.25;

•Spacecraft3 - A: 30,000 km; E: 0.7;

Once you have changed the Keplerian elements of each Spacecraft, it's time to move on to plotting the Spacecraft velocities. Also, since we do not need to report the orbital periods anymore, let's delete that FreeForm script editor:

•Delete "FreeForm: Report Orbital Periods" from the Mission Sequence

•Drag and drop a new FreeForm script editor into the while loop after the "Update" command

•Double-click the FreeForm script editor

•Rename it to "Plot Speeds"

For this FreeForm script editor, the code is relatively simple as well:

Plot Spacecraft1.ElapsedTime.ToHours, Spacecraft1.VMag, Spacecraft2.VMag, Spacecraft3.VMag;

Your Mission Sequence should look something like this:

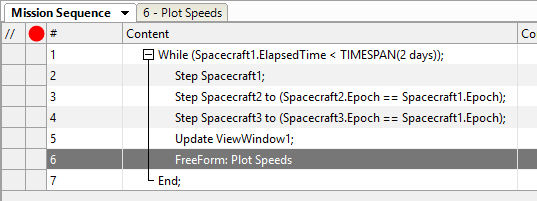
eTutorialMS

Mission Sequence Example

Save the Mission Plan, and then click run. After the Mission Sequence has concluded, try and answer these questions:

Which Spacecraft had the highest maximum velocity? Which Spacecraft had the lowest?

Run the Mission Plan again and look for the peak in velocity. Where in the Spacecraft's orbit did this occur?"

Looking at the graph, how does the orbital period of each Spacecraft compare?