The goal of single-objective optimization is to find the optimal solution that corresponds to the minimum or maximum value of a single objective function. In contrast, a multi-objective optimization problem involves multiple objective functions and will not generate a single best solution, but rather an array of best solutions commonly called the Pareto front.
Single-objective optimization utilizes a gradient descent approach to find an optimal solution. This approach uses derivatives and an iterative algorithm to hone in on the optimum value of the objective function. Multi-objective optimization utilizes a genetic algorithm, which is a type of stochastic search. This approach starts from a randomly generated population of candidate solutions then slowly improves the population via pseudo-random mutation and combination of solutions. The best solution candidates are selected for inclusion in the Pareto front. The Pareto front is an array of solutions that are nondominated, meaning that no one solution is better in all objectives than any other solution. In the image below, the Pareto front is depicted in red, showing the best solutions for an optimization problem that minimizes transit time and delta V. The solutions dominated by the Pareto front are depicted in grey.
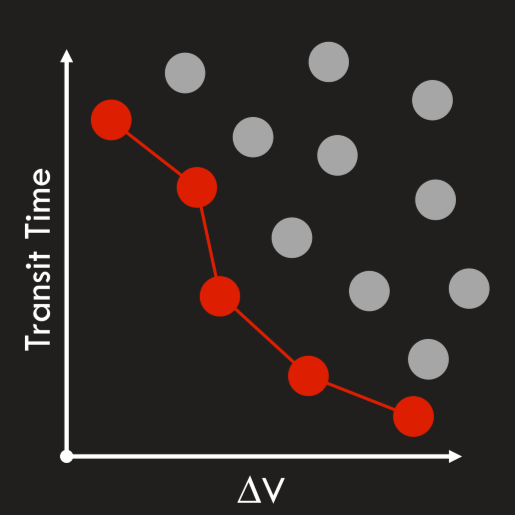
Pareto front of an optimization problem that minimizes transit time and delta V
Single-objective optimization state variables utilize an initial guess parameter, a scale parameter, and a perturbation parameter (used for evaluating numerical derivatives). Multi-objective optimization state variables do not require these parameters and allow integer state variables.
While single-objective optimization relies on constraints to set conditions that must be met for a solution to be considered feasible, multi-objective optimization problems do not have constraints since most stochastic solution methods do not handle them directly. Instead, constraint violations are tracked through additional objectives.
Both single-objective optimization and multi-objective optimization follow a similar workflow involving a problem configuration stage, a problem solve stage, then a solution retrieval stage. The basic components of the workflow are as follows:
1.Define the problem 2.Load the optimization engine 3.Create the evaluation loop 4.Retrieve the best solution |
See Also
|
•Using the Single-Objective Optimizer Guide •Using the Multi-Objective Optimizer Guide •Optimizer Properties and Methods •MultiObjectiveOptimizer Properties and Methods |