The built-in CovarianceUtilities object provides several static utility methods for working with a covariance matrix. It provides the capability to:
1.Generate random states based on a mean state and covariance matrix 2.Compute the mean state and/or covariance matrix from a series of random states 3.Compute the Mahalanobis distance of a state relative to a mean state and covariance matrix |
The CovarianceUtilities object assumes that the random states are normally distributed.
Generating Random States Based on a Covariance
The CovarianceUtilities.GetRandomState() and CovarianceUtilities.GetRandomStates() methods can be used to generate one or more random states based on an input mean state and covariance matrix. When using these methods, the mean state must have the same number of elements as the length of the diagonal of the covariance matrix.
These methods can be used as shown in the example script below.
// Generate the random states: Matrix randomStates = CovarianceUtilities.GetRandomStates(mySpacecraft.OD.Covariance.Matrix, {mySpacecraft.Position, mySpacecraft.Velocity}, /* Number of States to Generate */ 1000); |
The random states can then be displayed in a ViewWindow using a Formation object or propagated alongside the mean state if desired.
// Assign the states to members of a Formation for visualization: Formation myFormation; myFormation.Count = 1000; For i = 1 to myFormation.Count-1;
// The states are stored in each column of the randomStates Matrix.
// Assign the epoch: myFormation[i].Epoch = mySpacecraft.Epoch;
// Assign the position components: myFormation[i].Position = randomStates[0:2, i].ToArrayRowMajor();
// Assign the velocity components: myFormation[i].Velocity = randomStates[3:5, i].ToArrayRowMajor();
// Set the color: myFormation[i].Color = ColorTools.Lime;
End;
// Add a proximity zone to the Spacecraft to visualize its covariance: mySpacecraft.AddProximityZone("cov"); mySpacecraft.OD.Covariance.MapErrorEllipsoid(mySpacecraft.ProximityZones[0], 3);
// Visualize the Spacecraft and random states: View mySpacecraft, myFormation; |
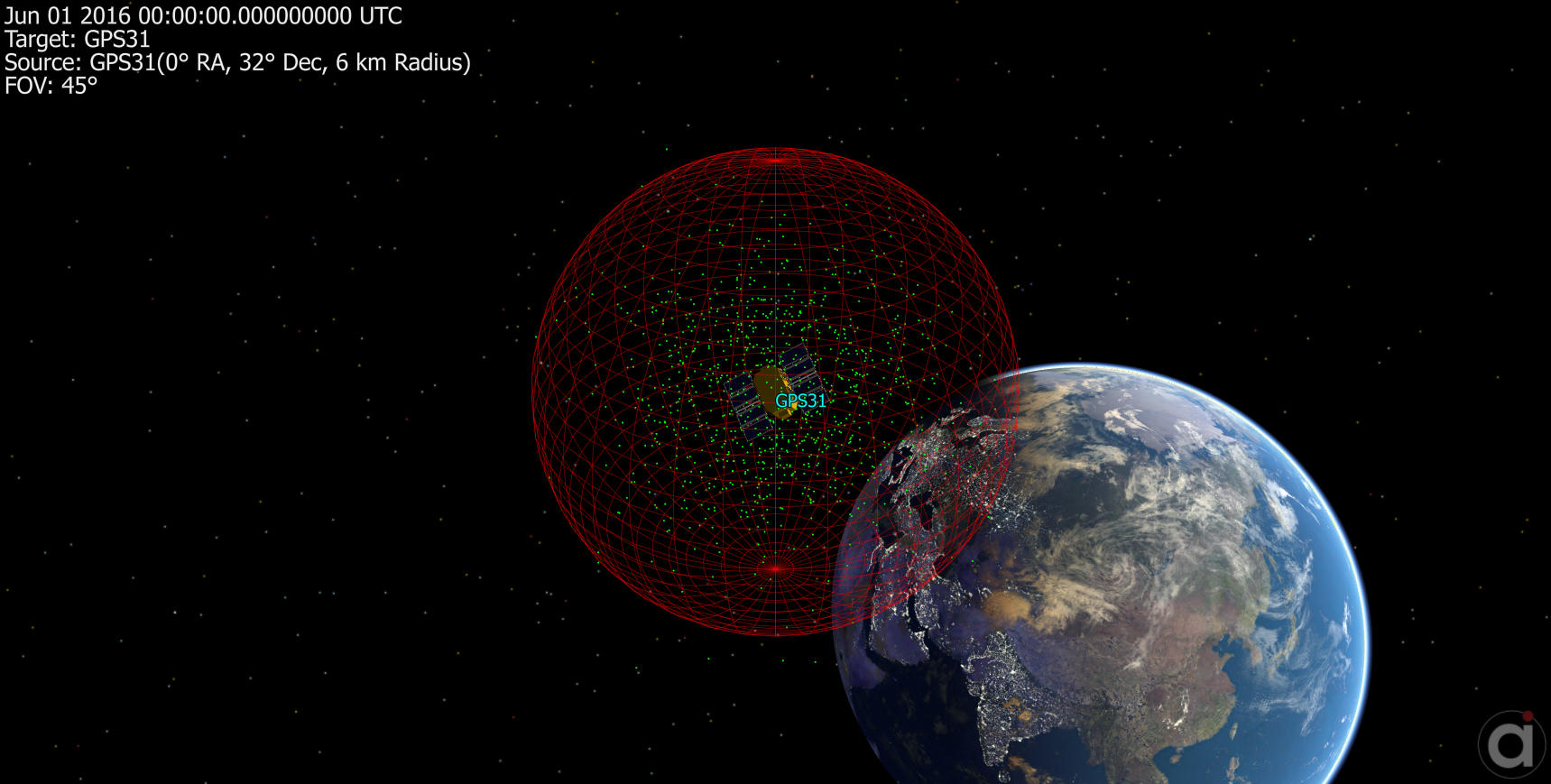
Random states generated using a Spacecraft covariance
Computing the Mean State and Covariance from a Distribution of States
The CovarianceUtilities.CalculateCovariance() and CovarianceUtilities.CalculateMeanAndCovariance() methods can be used to compute the covariance matrix and mean state from a set of normally distributed random states. All random state vectors must have the same number of elements, and number of elements will determine the dimension of the resulting mean state and covariance matrix.
These methods can be used as shown in the example below.
// Compute the covariance matrix from a set of random states: Matrix covarianceMatrix = CovarianceUtilities.CalculateCovariance(randomStates);
// Compute the covariance matrix from a Formation containing set of random states: covarianceMatrix = CovarianceUtilities.CalculateCovariance(myFormation); covarianceMatrix = CovarianceUtilities.CalculateCovariance(myFormation, "Equinoctial"); // Computes the covariance using the specified element set
// Compute the mean state and covariance matrix from a set of random states: Matrix covarianceMatrix = CovarianceUtilities.CalculateMeanAndCovariance(randomStates, meanState); // "meanState" is an output Array containing the mean state |
Computing the Mahalanobis Distance Using a Mean State and Covariance
The Mahalanobis distance is a non-dimensional measure of the distance between a state and a distribution. It takes into account the correlations of the distribution and is a representation of how many standard deviations the state is away from the mean of the distribution. The CovarianceUtilities.CalculateMahalanobisDistance() method can be used to compute the Mahalanobis distance for a state vector using a mean state and covariance matrix as in the example below.
// Calculate the Mahalanobis distance for a state: // Note: The "state" Array argument is the state for which to // compute the distance Variable mahalanobisDistance = CovarianceUtilities.CalculateMahalanobisDistance(meanState, covarianceMatrix, state); |
(1) Mahalanobis, Prasanta Chandra (1936). "On the Generalised Distance in Statistics". Proceedings of the National Institute of Sciences of India, p. 49-55.
See Also
•CovarianceUtilities Properties and Methods |